题目描述

给定一个多项式 ，请求出多项式展开后  项的系数。

输入格式

输入共一行，包含 5 个整数，分别为 a,b,k,n,m，每两个整数之间用一个空格隔开。

输出格式

输出共一行，包含一个整数，表示所求的系数。

这个系数可能很大，输出对 10007 取模后的结果。

输入输出样例

输入 #1

1 1 3 1 2

输出 #1

3

说明/提示

【数据范围】

对于 30% 的数据，有 0 ≤ k ≤ 10。

对于 50% 的数据，有 a = 1，b = 1。

对于 100% 的数据，有 0 ≤ k ≤ 1000，0 ≤ n,m ≤ k，n + m = k，0 ≤ a,b ≤ 。

NOIP 2011 提高组 day2 第 1 题。

---

一道二项式定理模板题

代码 ：

#include <bits/stdc++.h>
#define int long long 
using namespace std;

int a,b,k,n,m,C[1005][1005],mod = 10007;
signed main() {
	cin >> a >> b >> k >> n >> m;
	for (int i = 1; i <= k; i ++) {
		C[i][0] = C[i][i] = 1;
		for (int j = 1; j <= i-1; j ++) C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
	}
	int ans = C[k][m];
	a %= mod, b %= mod;
	int x = 1 ,y = 1;
	for (int i = 1; i <= n; i ++) x = x * a % mod;
	for (int i = 1; i <= m; i ++) y = y * b % mod;
	ans = ans * x % mod * y % mod;
	cout << ans % mod;
	return 0;
}

二项式定理 ：

  

代码解说 ：

1. 计算组合数

for (int i = 1; i <= k; i ++) {
    C[i][0] = C[i][i] = 1;
    for (int j = 1; j <= i-1; j ++) C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
}

• 这个循环用于计算组合数  ，即从 i 个元素中选出 j 个元素的组合数。

• C[i][0] = C[i][i] = 1：当 j=0 或 j=i 时，组合数为 1。

• C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod：根据组合数的递推公式 C[i][j]=C[i−1][j−1]+C[i−1][j]，计算组合数并对结果取模。

2. 计算二项式系数

int ans = C[k][m];

• C[k][m] 表示从 k 个元素中选出 m 个元素的组合数，即二项式系数 C(k,m)。

3. 对 a 和 b 取模

a %= mod, b %= mod;

• 对 a 和 b 取模，避免后续计算中数值过大。

4. 计算 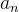 和

int x = 1 ,y = 1;
for (int i = 1; i <= n; i ++) x = x * a % mod;
for (int i = 1; i <= m; i ++) y = y * b % mod;

• x 用于计算  mod 。

• y 用于计算  mod 。

5. 计算最终结果

ans = ans * x % mod * y % mod;

• 最终结果是二项式系数 C[k][m] 乘以  和 ，并对结果取模。

 

总结

核心是计算二项式展开式  中  项的系数，并对结果取模 10007。代码通过递推公式计算组合数，并通过循环计算幂次，最终得到结果并输出。