蒟蒻第一次写题解，写的不好多担待qwq

A. Treasure Hunt

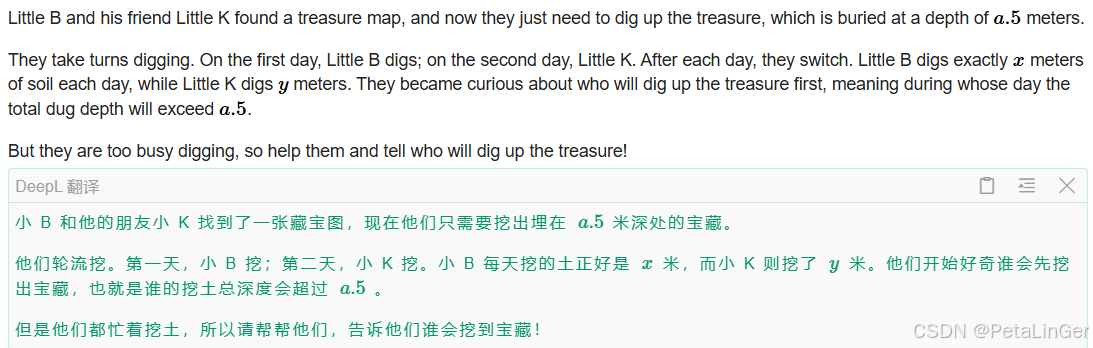没什么好说的，对(x+y)取模，然后对x进行一次比较即可

void solve() {
	ll x, y, a, sum;
	cin >> x >> y >> a;
	sum = x + y;
	a %= sum;
	if (x > a) {
		cout << "NO\n";
	} else {
		cout << "YES\n";
	}
}

B. Pushing Balls

显而易见，每个球只能在其所在一行的左侧或上方全部有球时，该球合法

注意类似此图的(4,2)无法成立即可

思路：写一个行和列的数组判断这行或这列是否还能塞球即可，代码如下

void solve() {
	int n, m;
	string s;
	cin >> n >> m;
	vvi tu(n + 1, vi(m + 1));
	vi hang(n + 1, 1);
	vi lie(m + 1, 1);
	int pd{0};
	for (int i = 1; i <= n; ++i) {
		cin >> s;
		if (!pd) {
			for (int j = 1; j <= m; ++j) {
				tu[i][j] = s[j - 1] - '0';
				if (tu[i][j] == 1) {
					if (hang[i] != 1 && lie[j] != 1) {
						pd = 1;
						break;
					}
				} else {
					hang[i] = 0;
					lie[j] = 0;
				}
			}
		}
	}
	if (pd) {
		cout << "NO\n";
	} else {
		cout << "YES\n";
	}
}

C. Dining Hall

题目说人话就是ti=1的客人会坐在最近的空位上，ti=0的客人会坐在最近的空桌上，问每个人位置

打表，图中0为过道，数字为从(0,0)出发坐到每个位置的行动距离

可发现ti=0只会坐在距离为对3取模为1的位置，ti=1会坐在距离最近同时依据(x,y)排序最小的位置

考虑到n的规模最多为50000，即最多有50000桌被占用，考虑先把每桌的距离算下来再填人

    cin >> n;
	map<int, queue<pii>> ivp;
	int x{0}, y{0}, cnt{1}, ccnt{1};
	for (int i = 0; i < n; ++i) {
		int l = (x + y) * 3;
		ivp[l + 1].push({x * 3 + 1, y * 3 + 1});
		ivp[l + 2].push({x * 3 + 1, y * 3 + 2});
		if (y != 0) {
			ivp[l + 2].push({x * 3 + 2, y * 3 - 1});
			ivp[l + 2].push({x * 3 + 2, y * 3 + 1});
			y--, ++x;
		} else {
			ivp[l + 2].push({x * 3 + 2, y * 3 + 1});
			y = x + 1, x = 0;
		}
	}

初始化，用队列和排序解决(x,y)排序最小的位置

	for (int i = 0; i < n; ++i) {
		cin >> inp;
		if (inp == 1) {
			while (ivp[cnt].empty()) {
				++cnt;
			}
			auto [a, b] = ivp[cnt].front();
			ivp[cnt].pop();
			cout << a << " " << b << "\n";
		} else {
			while (ivp[ccnt].empty()) {
				ccnt += 3;
			}
			auto [a, b] = ivp[ccnt].front();
			ivp[ccnt].pop();
			cout << a << " " << b << "\n";
		}
	}

然后根据输入，寻找最近的空位即可

D. Simple Permutation

众所周知，构造题想出来就不难，简单说一下思路 设i为素数

那我连续输出i i-1 i+1 i-2 i+2 i-3 i+3 ……一定符合题意

所以题目就改为寻找一个>=n/3&&<=n/2的素数 n<=10^5 用最简单的线性筛即可

const int N = 100005;
int cnt{0}, prime[N], vis[N];
void get_prime() {
	for (int i = 2; i <= N; ++i) {
		if (!vis[i])prime[++cnt] = i;
		for (int j = 1; j <= cnt && i * prime[j] <= N; ++j) {
			vis[i * prime[j]] = 1;
			if (i % prime[j] == 0)break;
		}
	}
	return ;
}

E1. Canteen (Easy Version)

简单想就是向前换位相减，直到a数组为0即可，但因为n<=2*10^5 硬模拟O(n*n)超时

考虑先对a数组b数组相减 pri=ai-bi 然后对pri进行前缀和

如果prj<=pri 则从i-j ai能被消为0，所以题意就转为寻找对于每个i位置能让prj<=pri的最大j-i差值

（PS:这是个环，所以求前缀和时需要n*2再加一遍）

又因为如果存在i<z<j prz>pri prj<=pri成立 =》prz<prj成立 但j-z<j-i

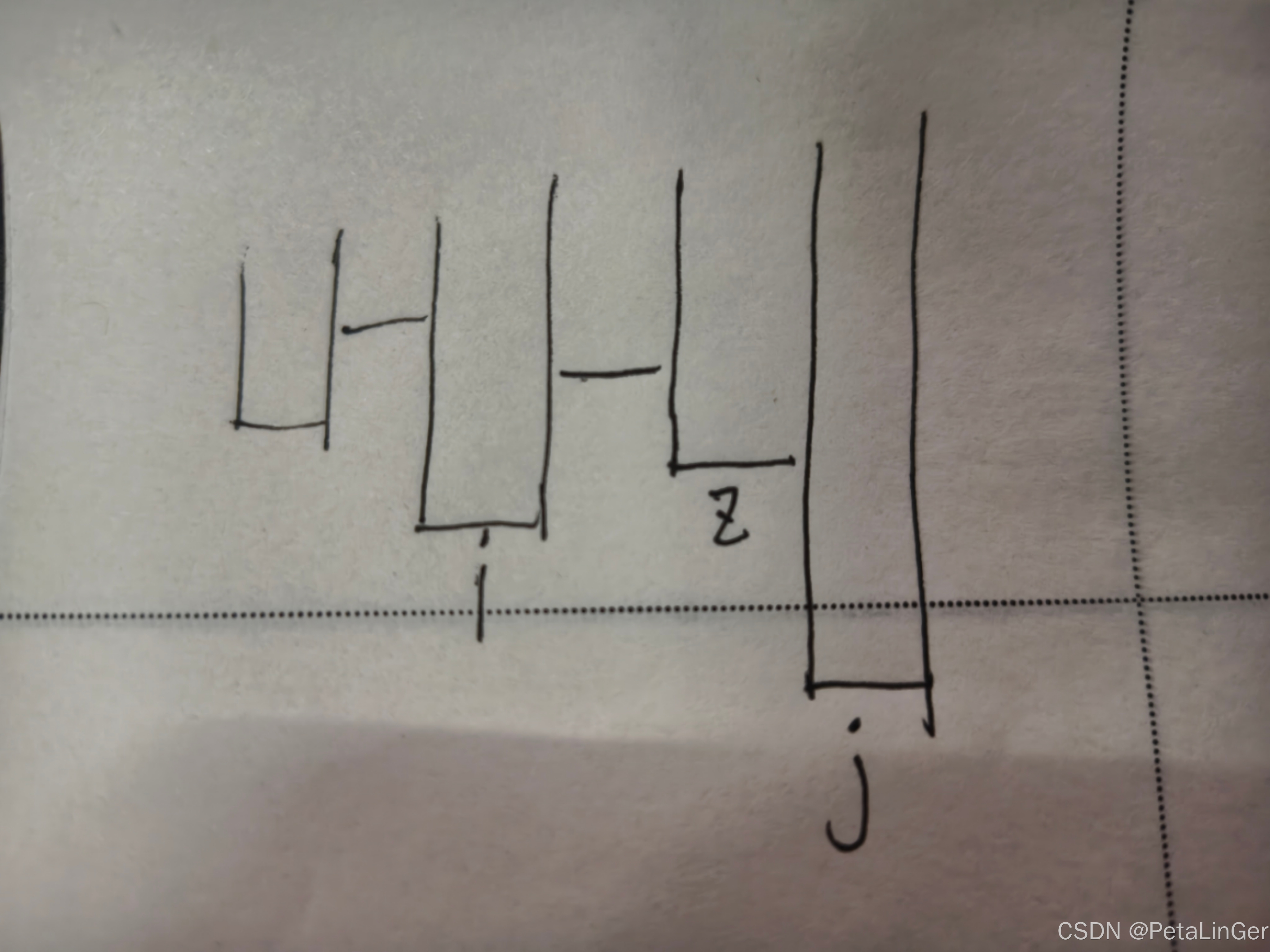
所以又可以将题目改为寻找最长非递增序列中j-i的最大差值，每次寻找比当前最小值小的即可

代码如下

void solve() {
	int n, k, ans{1}, chapos = 1;
	ll chamin;
	cin >> n >> k;
	vl a(n + 1), b(n + 1);
	vl pr(2 * n + 1, 0);
	map<ll, int> mp;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	cin >> b[1];
	chamin = a[1] - b[1], pr[1] = chamin;
	for (int i = 2; i <= n; ++i) {
		cin >> b[i];
		pr[i] = pr[i - 1] + a[i] - b[i];
		if (chamin >= pr[i]) {
			cmax(ans, i - chapos);
			chamin = pr[i], chapos = i;
		}
	}
	for (int i = n + 1; i <= 2 * n; ++i) {
		pr[i] = pr[n] + pr[i - n];
		if (chamin >= pr[i]) {
			cmax(ans, i - chapos);
			chamin = pr[i], chapos = i;
		}
	}
	cout << ans << "\n";
}