P1955 NOI2015 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_1,x_2,x_3,\cdots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_i=x_j$ 或 $x_i\ne x_j$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\ne x_1$，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 $t$，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 $n$，表示该问题中需要被满足的约束条件个数。接下来 $n$ 行，每行包括三个整数 $i,j,e$，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 $e=1$，则该约束条件为 $x_i=x_j$。若$e=0$，则该约束条件为 $x_i\ne x_j$。

输出格式

输出包括 $t$ 行。

输出文件的第 $k$ 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 $k$ 个问题判定为可以被满足，NO 表示不可被满足。

输入输出样例 #1

输入 #1

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出 #1

NO
YES

输入输出样例 #2

输入 #2

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出 #2

YES
NO

说明/提示

【样例解释1】

在第一个问题中，约束条件为：$x_1=x_2,x_1\ne x_2$。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：$x_1=x_2,x_1=x_2$。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：$x_1=x_2,x_2=x_3,x_3=x_1$。只需赋值使得 $x_1=x_2=x_3$，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\ne x_1$。由前三个约束条件可以推出 $x_1=x_2=x_3=x_4$，然而最后一个约束条件却要求 $x_1\ne x_4$，因此不可被满足。

【数据范围】

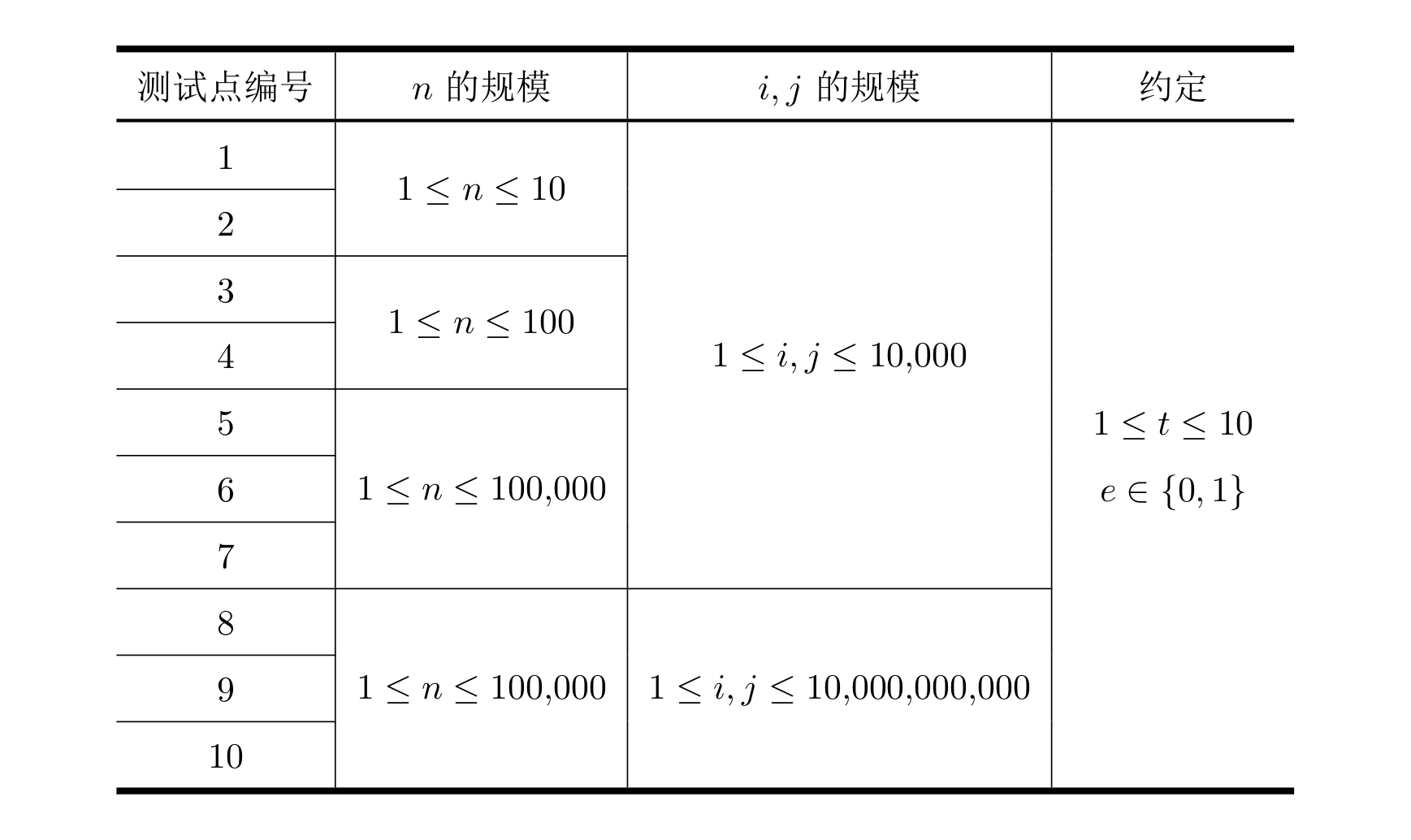
所有测试数据的范围和特点如下表所示：

勘误：测试点 $8\sim 10$ 的 $i,j$ 约束为 $1\le i,j\le 10^9$，而不是下图中的 $10^{10}$。

思路

前置知识：

• 并查集，哈希表，离散化 （都是可以点击的链接，是我挑选的，不是csdn自带的搜索）

刚看感觉和种类并查集有点像，和关押罪犯那题很像，但是有问题，就是不等于的关系是不可以传递的。a!=b, b!=c，不能说明a和c相等！我一开始就是因为这个错了。

应该先把所有的e=1的数据合并了，然后再判断e=0的数据。如果i和j在一个集合，那就输出NO

最后一个问题，显然不能开10^9的数组，所以要么使用离散化要么使用哈希，可以点击前置知识中的链接。

代码

我忘了离散化这个东西了，所以就用了hash，想看离散化实现的可以去点击前置知识的链接

为什么用快读是因为我看我的做法总时长1.17s，题解里面的做法三百多毫秒，不知道为什么差距这么大。然后试着用了一下快读，发现我也325ms。我之前都看不起用快读的人，因为我不打算法竞赛，我只会用std::cin。现在用了才知道真香。

#include <iostream>
#include <cstring>    //memset
#include <algorithm>
#define M 200003
using i64 = long long;

inline int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while(ch>'9'||ch<'0'){
		if(ch=='-') f = -1;
		ch = getchar();
	}
	while(ch<='9'&&ch>='0'){
		x = x * 10 + ch-'0';
		ch = getchar();
	}
	return x*f;
}
int t, n;
struct que{
	int x; int y; int e;
} qs[100005];

struct node{
	int key;
	int nxt;
} data[200005];
int head[200005];
int parent[200005];

int cnt;

int find(int x)
{
	if(parent[x]!=x)
	{
		parent[x] = find(parent[x]);
	}
	return parent[x];
}

void unionset(int x, int y)
{
	int rx = find(x);
	int ry = find(y);
	if(rx==ry) {return ;}
	parent[rx] = ry;
}

int f(int key)
{
	return (key%M+M)%M;
}
int get_num(int key)
{
	for(int i = head[f(key)];i!=0; i = data[i].nxt)
	{
		if(data[i].key == key)
		{
			return i;
		}
	}
	return 0;
}
int add(int key)
{
	int num = get_num(key);
	if(num!=0) {return num;}
	int idx = f(key);
	data[++cnt].nxt = head[idx];
	head[idx] = cnt;
	data[cnt].key = key;
	return cnt;
}
bool cmp(que q1, que q2)
{
	return q1.e>q2.e;
}
int main()
{
	// std::cin>>t;
	t = read();
	for(int j = 1; j<=t; j++)
	{
		memset(data, 0, sizeof(data));
		memset(head, 0, sizeof(head));
		memset(parent, 0, sizeof(parent));
		memset(qs, 0, sizeof(qs));
		cnt = 0;       //一定要记得重置这些，如果不使用类的话
		for(int i = 1; i<=200004; i++)
		{
			parent[i] = i;
		}

		// std::cin<<n;
		n = read();
		for(int i = 1; i<=n; i++)
		{
			// std::cin>>qs[i].x>>qs[i].y>>qs[i].e;
			qs[i].x = read(); qs[i].y = read(); qs[i].e = read();
			add(qs[i].x); add(qs[i].y);
		}
		std::sort(qs+1, qs+n+1, cmp);
		int flag = 0;
		for(int i = 1; i<=n; i++)
		{
			if(qs[i].e==1)
			{
				unionset(get_num(qs[i].x), get_num(qs[i].y));
			}
			else{
				if(find(get_num(qs[i].x))==find(get_num(qs[i].y)))
				{
					flag = 1; std::cout<<"NO\n"; break;
				}
			}
		}
		if(flag==0) {std::cout<<"YES\n";}
	}
	return 0;
}

解释

不懂哈希表的可以点击前文的链接，或者这里的