例题

现需要遍历全国共34个直辖市/省会/自治区首府，请设计遍历方案，访问每一座城市一次，并最终回到起始城市，且总路径最短。

问题分析

模型假设：遍历过程中，两两城市之间的直线距离视为遍历时的路径距离。将每个目的地看作节点，每条路径看作边，整个问题就是图论问题。

论文中模型假设怎么写？从两方面思考：在现实中可行，能简化题目。

现实中，两两城市之间可以走高速、坐飞机、走国道等等，不同的交通方式都可以实现遍历。本条假设中“直线距离”视为城市间的路径距离，在现实中可以搭乘飞机实现，而且数据更容易查到，简化了问题；

可行解：即所有能实现遍历的方案，共34 个城市，则有34！种可行方案（34的阶乘种）。我们需要从这么多种方案里，挑选出总路径最短的那一个。

简单粗暴法：从第34个城市里任选一个作为起点，下一站从剩余33个城市里选一个；……；求出所有可能方案的路径的总长度，再判断其中的最小值。在这过程中需要先求出所有顶点的全排列。

学过数据结构的同学都知道，在时间复杂度上，阶乘是比指数函数还要可怕的存在。34的阶乘计算次数的数量级在10^(38)。

因此我们应当尽量降低复杂度，否则城市数量多的话，可能比赛期间代码压根运行不完。

自然界中的启发

简单粗暴法的时间复杂度实在太高了。不妨参考下自然界的生物是如何解决类似问题的。

自然界的蚂蚁在觅食时，也需要面临类似的问题：某处有食物，但在面临选择时（例如有大石头挡路不得不绕行），选择哪条路能使到达目的地的路径最短呢？

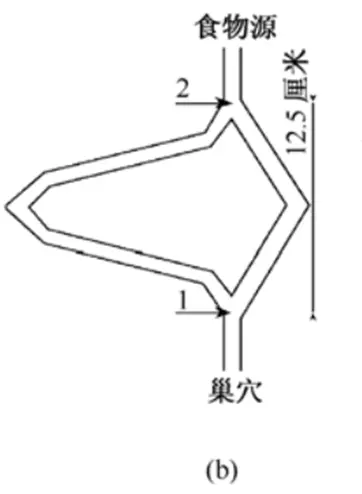
这与例题很类似：都是在面临多条路径时，选择下一条路。

现实中：

1. 蚁群在觅食时，每只蚂蚁在走过的路径上会留下一种称为信息素的物质
2. 在路径分叉口时面临选择：走左边路径还是右边路径？
3. 概率：蚂蚁在选择路径时总是倾向于信息素浓度高的方向移动
4. 一只蚂蚁的信息素总量视为有限的常数，则蚂蚁走过的路径越短、留在路径上的信息素浓度越高
5. 而信息素本身会随着时间不断挥发

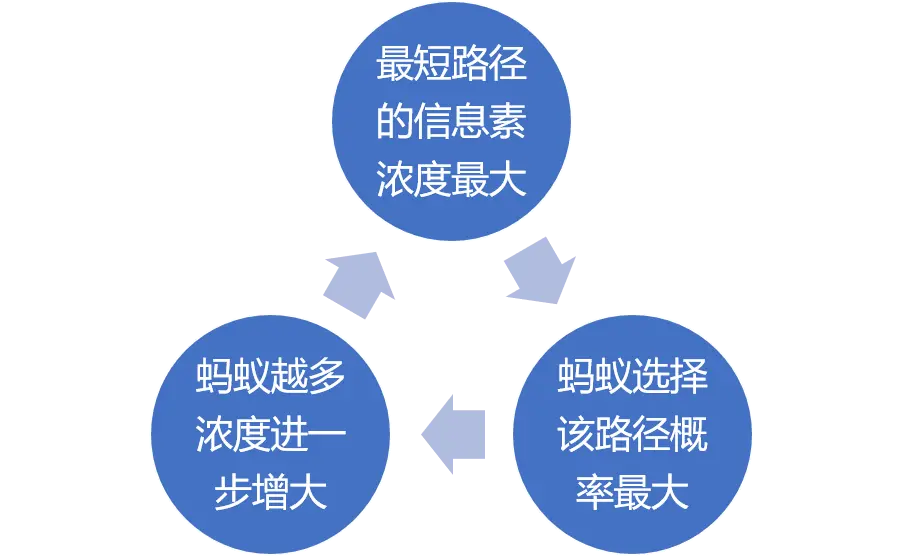
根据以上五条，可以推导与现实相符的出结论：

• 距离长的路径走过的蚂蚁少、后期信息素浓度增加量小于挥发量，总的变化是减少的
• 距离短的路径走过的蚂蚁多、后期信息素浓度增加量大于挥发量，总的变化是增加的

因此形成了一个正反馈迭代：

距离短的路径信息素浓度高

⇒后续蚂蚁选择该路径的概率更大

⇒距离短的路径上信息素浓度进一步升高

如此正反馈，整个蚁群最终走在了最短的路径上。

 

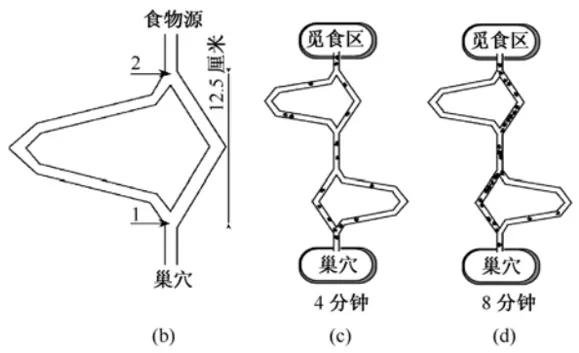
思考：蚁群能保证在所有情况下得到的一定是最短路径么？

同理，我们可以仿照蚁群的方法：

• 参数初始化，设置蚁群、城市距离等参数；
• 从某一城市作为起点释放出蚁群，每只蚂蚁不断选择下一个前往的城市；
• 经过多次迭代，每一次迭代都更新信息素影响下一次迭代时蚁群的选择；
• 达到迭代终止条件后，输出求得的最短遍历方案。

（未完待续，下一篇讲解实现蚁群算法的4步）