扫描线

处理逻辑

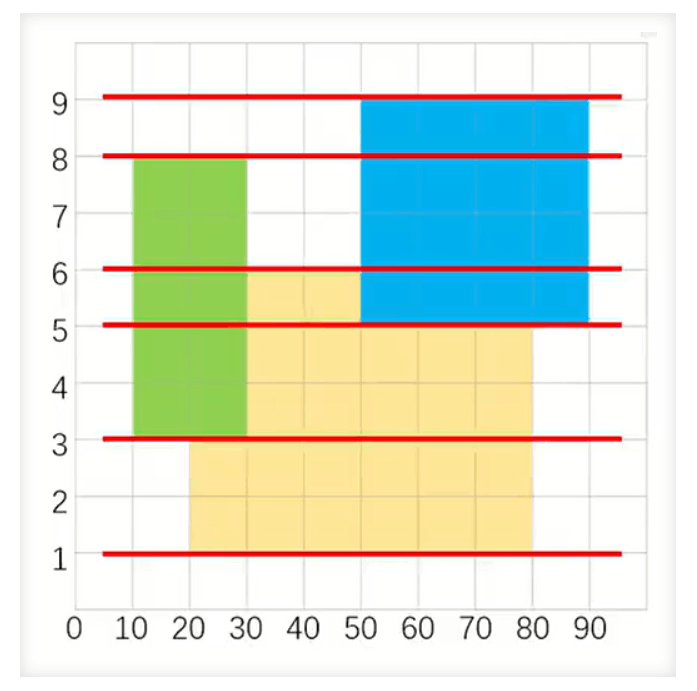
1、就是一根线,从下往上扫,以每个矩形的上下边为界，把 n 个矩形组成的区域分割成 2n - 1个区块
2、区块的高度就是扫过的距离,即y[i + 1] - y[i]
3、区块长度就是区块内矩形长度的并,即 len[i]
4、面积并 = ∑{len[i] * (y[i + 1] - y[i])}     
5、区块长度可以用线段树进行维护
  每当扫到一个矩形的下边时,就加入该矩形长度的贡献    
  每当扫到一个矩形的上边时,就减少该矩形长度的贡献    
6、区块长度需要通过矩形的 x 坐标来拼凑 

P5490 【模板】扫描线 & 矩形面积并

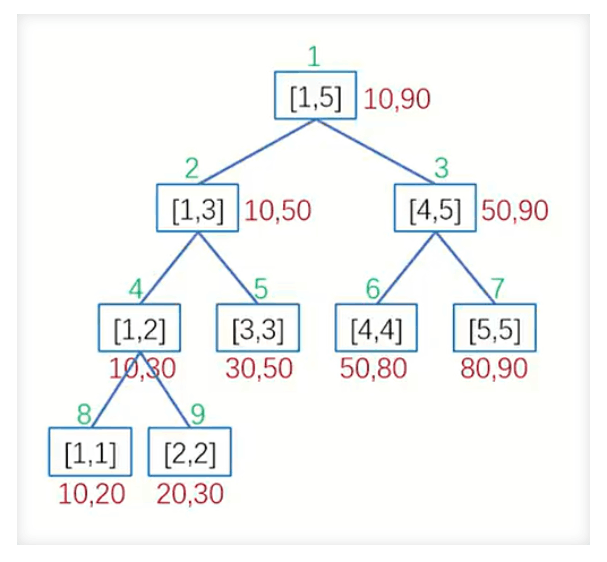
观察上方例子，在线段树合并的过程中,如果以下标直接进行合并
会发现[1,5] 区间值是下标连续，但是对应的 x 坐标之间会有空隙 所以不能直接一一映射

这里引入一种技巧，右端点偏移映射
也就是 正常[1,3] 区间对应的 x 坐标为 [10,30]
但是在处理上映射的结果是 [10,50] -- 也就是 
[L,R] --> [Xl,Xr+1]
通过这种方式实现的映射,下标是连续的，同时对应的 x 坐标也是连续的

len[u] =
  (1) Xr+1 - Xl，(cnt > 0)
  (2) len[ls] + len[rs] ,(cnt = 0)

解释 :
 当 cnt > 0 时，说明这个区间被覆盖,可以直接通过 x 的坐标差求值计算 
当 cnt = 0 时，说明没有完全覆盖，要用左右儿子进行拼凑

特殊的由于在存储的时候是右偏移一位实现的，那对应在传参进行查询是，右端点就需要 - 1回调到正确的位置

例子

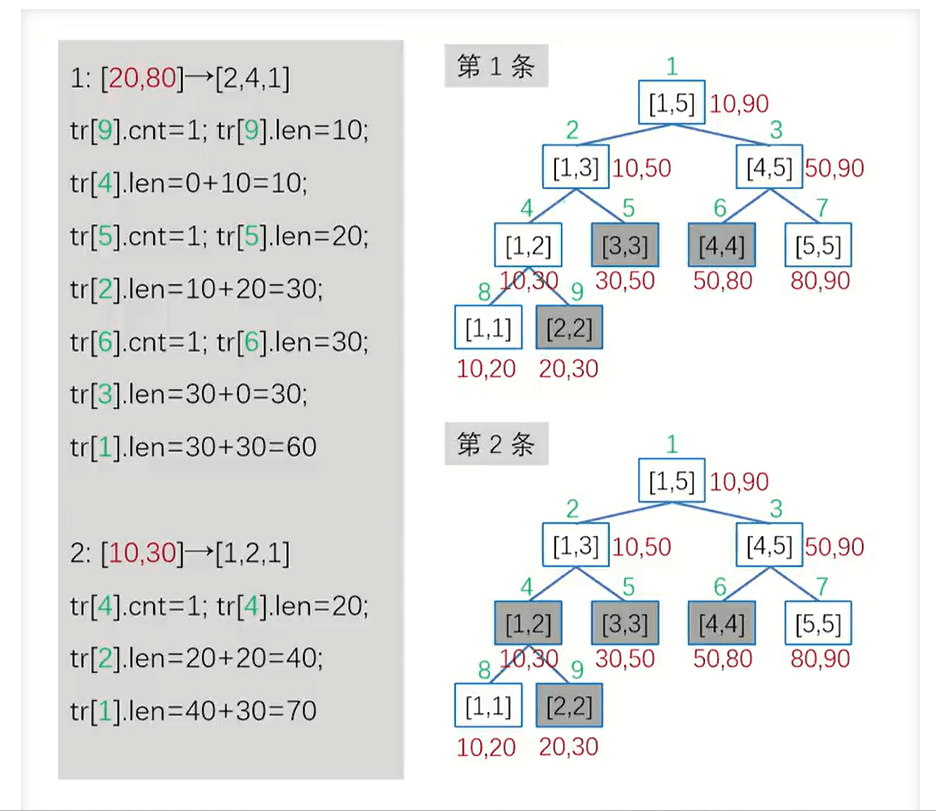
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
// 扫描线 
struct line{
    int x1,x2,y;
    //用来区分边的类型， 1为入边,-1为出边
    int tag;  
    // 以高度进行排序,方便枚举 
    bool operator < (const line & t) const{
        return y < t.y;
    }
}L[N];
struct node{
    int l,r;
    // cnt 用来描述当前区间的覆盖次数,len 用来表示覆盖的长度 
    int cnt,len;
}tr[N * 8] ; // 四倍不够，会越界，要开 8 倍 
int X[N];

void pushup(int u){
    int l = tr[u].l,r = tr[u].r;
    if(tr[u].cnt) tr[u].len = X[r + 1] - X[l];
    else tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

void build(int u,int l,int r){
    tr[u] = {l,r,0,0};
    if(l == r) return;
    int mid = l + r >> 1;
    build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
    pushup(u);
}
// 区间修改 
void update(int u,int l,int r,int tag){
    if(l > tr[u].r || r < tr[u].l) return ;
    if(l <= tr[u].l && tr[u].r <= r){
        tr[u].cnt += tag;
        pushup(u);
        return ; 
    }
    update(u << 1,l,r,tag);
    update(u << 1 | 1,l,r,tag);
    pushup(u);
}
int main(){
    int n,x1,x2,y1,y2;
    cin >> n;
    for(int i = 1;i <= n;i ++){
        cin >> x1 >> y1 >> x2 >> y2;
        // 记录入线和出线(前面那条和后面那条) 
        L[i] = {x1,x2,y1,1};
        L[i + n] = {x1,x2,y2,-1};
        X[i] = x1,X[n + i] = x2; 
    }
    n <<= 1;
    // 离散化的基本操作 : 排序,去重,二分 
    sort(L + 1,L + n + 1);
    sort(X + 1,X + n + 1);
    int m = unique(X + 1,X + 1 + n) - X - 1;
    build(1,1,m - 1);
    long long ans = 0;
    for(int i = 1;i < n;i ++){
        int l = lower_bound(X + 1,X + m + 1,L[i].x1) - X;
        int r = lower_bound(X + 1,X + m + 1,L[i].x2) - X; 
        update(1,l,r - 1,L[i].tag);
        ans += 1ll * tr[1].len * (L[i + 1].y - L[i].y); 
    }
    cout << ans;
    return 0;
}

P1856 [IOI 1998 ] [USACO5.5] 矩形周长Picture

#include <bits/stdc++.h>
#define int long long
#define ls u << 1
#define rs u << 1 | 1 
using namespace std;
const int N = 1e5 + 5;
struct line{
    int l,r,y;
    int tag;
    bool operator < (const line &t) const{
        if(y == t.y) return tag > t.tag;
        return y < t.y;
    }
}L[N];
struct node{
    int l,r,cnt,len;
    int sum; // 区间覆盖竖边的条数
    int lcover,rcover; 
}tr[N * 8];
int X[N];
int n,ans,last;
void pushup(int u){
    int l = tr[u].l, r = tr[u].r;
    if(tr[u].cnt){
        tr[u].len = X[r + 1] - X[l];
        tr[u].sum = 2;
        tr[u].lcover = 1;
        tr[u].rcover = 1;
    }
    else{
        tr[u].len = tr[ls].len + tr[rs].len;
        tr[u].sum = tr[ls].sum + tr[rs].sum;
        tr[u].lcover = tr[ls].lcover;
        tr[u].rcover = tr[rs].rcover;
        if(tr[ls].rcover && tr[rs].lcover) tr[u].sum -= 2;
    }
} 
void build(int u,int l,int r){
    tr[u] = {l,r,0,0,0,0,0};
    if(l == r) return;
    int mid = l + r >> 1;
    build(ls,l,mid);
    build(rs,mid + 1,r);
    pushup(u);    
}
void update(int u,int l,int r,int tag){
    if(tr[u].l >= l && tr[u].r <= r){
        tr[u].cnt += tag;
        pushup(u);
        return;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if(l <= mid) update(ls,l,r,tag);
    if(r > mid) update(rs,l,r,tag);
    pushup(u); 
}
signed main(){
    cin >> n;
    for(int i = 1;i <= n;i ++){
        int x1,x2,y1,y2;
        cin >> x1 >> y1 >> x2 >> y2;
        L[i] = {x1,x2,y1,1};
        L[i + n] = {x1,x2,y2,-1};
        X[i] = x1,X[i + n] = x2;
    }    
    n <<= 1;
    sort(L + 1,L + 1 + n);
    sort(X + 1,X + 1 + n);
    int m = unique(X + 1,X + 1 + n) - X - 1; 
    build(1,1,m - 1); 
    for(int i = 1;i < n;i ++){
        int l = lower_bound(X + 1,X + 1 + m,L[i].l) - X;
        int r = lower_bound(X + 1,X + 1 + m,L[i].r) - X;
        update(1,l,r - 1,L[i].tag);
        ans += abs(tr[1].len - last); // 横边 
        last = tr[1].len;
        ans += tr[1].sum * (L[i + 1].y - L[i].y); // 竖边 
    }
    // 最后一条边 
    ans += L[n].r - L[n].l;
    cout << ans;
    return 0;
}