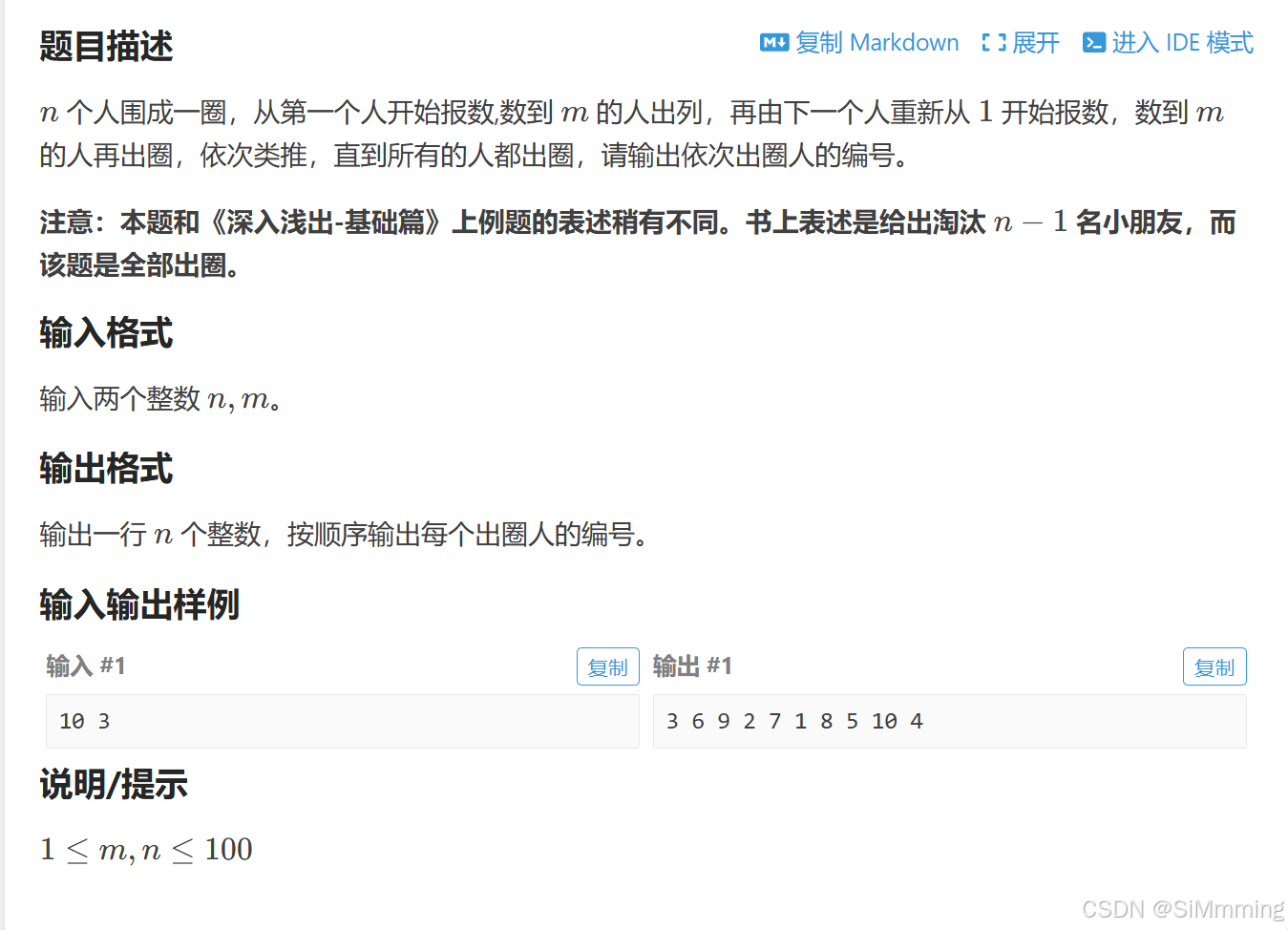
题目一 P1996 约瑟夫问题【普及-】

P1996 约瑟夫问题 - 洛谷

AC代码1

#include <bits/stdc++.h>
const int N = 105;
//静态链表
struct Node {
	int id;
	int nextid;
}node[N];
int main()
{
	int n, m; scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) { node[i].id = i; node[i].nextid = i + 1; }
	node[n].nextid = 1;//循环链表
	int prev=1; int now=1;//单向二指针
	//剩余人数大于一人重复
	while ((n--) > 1)
	{
		//数m个，边数边移动prev和now
		//没有等于，当前now指向下一个，向后移动m-1个即可
		for (int i = 1; i < m; i++) { prev = now; now = node[now].nextid; }
		printf("&d ", node[now].id);
		//删除
		node[prev].nextid = node[now].nextid;//跳过now
		now = node[prev].nextid;//从下个继续开始数
	}
	printf("%d", node[now].id);
	return 0;
}

• 从1开始给链表结点赋值是为了更好的模拟位置id
• 单向链表定义二指针
• 删除链表结点即跳过当前结点，pre.next=now.next

AC代码2(better)

#include <bits/stdc++.h>
using namespace std;
queue <int> q;//不用提前规定长度，可以是变长的
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) q.push(i);
    while (!q.empty())
        {
            //没轮到
            for (int i = 1; i < m; i++) {
                int t = q.front();//注意语法
                q.push(t);
                q.pop();
            }
            //轮到
            cout << q.front() << " ";
            q.pop();
        }
    return 0;
}

• 使用队列模拟，如果没轮到就下一轮
• 注意队列的语法front,pop,push
• 若是使用链表，这题的代码实现复杂程度无疑大大上升了，其实，我们完全用不着那么麻烦，一个个地报数，可以想象成一个队列，一个人报完数后，判断他所报的数是不是出局的数，如果是，直接弹出，但若不是，将其移动至队尾

题目二 P1160 队列安排【普及/提高-】

P1160 队列安排 - 洛谷

AC代码1

#include <bits/stdc++.h>
using namespace std;
const int N = 10e5 + 10;
int n,m;
set<int> s;//需要删除的人
struct Node {
	int id;
	int preid=-1;
	int nextid=-1;
}node[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)node[i].id = i;
	//插入
	for (int i = 2; i <= n; i++)
	{
		int num, lr;
		cin >> num >> lr;
		if (lr == 0)
		{
			//插入到左边，从左边开始改指针
			//注意插入到左边时一定要考虑左边有没有前驱节点
			if (node[num].preid == -1) { // num is the head
				node[i].preid = -1;
				node[i].nextid = num;
				node[num].preid = i;
			}
			else { 
				int pre = node[num].preid;
				node[pre].nextid = i;
				node[i].preid = pre;
				node[i].nextid = num;
				node[num].preid = i;
			}
		}
		else
		{
			//插入到右边，从右边开始改指针
			//同理考虑有没有后继结点
			if (node[num].nextid == -1) { 
				node[i].preid = num;
				node[i].nextid = -1;
				node[num].nextid = i;
			}
			else { // num has a successor
				int nxt = node[num].nextid;
				node[nxt].preid = i;
				node[i].nextid = nxt;
				node[i].preid = num;
				node[num].nextid = i;
			}
		}
	}
	//存入要删除的人
	cin >> m;
	for (int i = 0; i < m; i++)
	{
		int t; cin >> t;
		s.insert(t);
	}
	// Delete each node in the set
	//遍历s中的每一个结点
	for (int x : s) {
		int pre = node[x].preid;
		int nxt = node[x].nextid;

		// Adjust the links of predecessor and successor
		if (pre != -1) {
			node[pre].nextid = nxt;
		}
		if (nxt != -1) {
			node[nxt].preid = pre;
		}
		//node[x].preid = -1;
		//node[x].nextid = -1;
	}
	// Find the head of the list
	//遍历链表，找到头节点
	int head = 1;
	while (node[head].preid != -1) {
		head = node[head].preid;
	}
	// Traverse from head to tail
	int now = head;
	while (now != -1) {
		cout << now << " ";
		now = node[now].nextid;
	}
	return 0;
}

• 注意审题：像这种频繁的用到插入和删除的，一般都是要用链表模拟的
• 对前驱和后继进行操作时一定要先判断前驱和后继是否存在，主要错误之1

• 擅用临时变量代指
• 本题涉及到频繁的插入和删除，并且每一个结点既可能对前驱也可能对后继操作，所以用到双向链表
• set：用在此处的目的是去重，进一步提高时间效率，还可以用unordered_set，减少排序的时间复杂度，注意set的用法：①insert②erase③find，注意find 返回一个迭代器，如果元素存在，迭代器指向该元素，否则返回 end()，所以判断是否找到某个元素应该用s.find(x)和s.end(）作比较，④.size()，⑤（左闭右开区间）

auto range = s.equal_range(5);  // 查找元素 5 的区间
cout << "Lower bound: " << *range.first << ", Upper bound: " << *range.second << endl;

• 注意：这里不能将被删除结点的信息全部删除

• 

• 因为下面寻找头节点的逻辑中需要用到

• 如果被删除的是头节点1，并且它的全部信息也在上面被设置为-1了，那么链表就从这里断开了，找不到前面有哪些节点了，实际上保留被删除结点的相关信息是可行的，因为在删除结点的过程中已经将这个结点跳过了，所以实际上连在一起的链表中也不会存在被删除的结点。如果不保留，可能导致如果设置的head被删除了，它不在链表中了，那么链表的其它所有信息也就都丢失了