P6886 [COCI 2016/2017 #3] Meksikanac

题目描述

Norman 有一个给定的 $K$ 边形的苍蝇拍。他想知道有多少种放置苍蝇拍的方法，使得这个苍蝇拍的顶点在顶点为 $(0,0)$ 和 $(X_p,Y_p)$ 的矩形中，并且各个顶点是整点，满足没有一个苍蝇被伤害。

其中，整点的定义是横坐标和纵坐标都是整数的点。

这个矩形中有 $N$ 个苍蝇，每一个苍蝇可以看成一个点 $(X,Y)$。一个苍蝇会被伤害，当且仅当这个苍蝇在这个苍蝇拍的顶点，边或内部。

苍蝇拍不能旋转或翻折。

输入格式

第一行包含三个正整数 $X_p,Y_p,N$，意义同上。

以下 $N$ 行，每行包含两个正整数 $(X,Y)$，表示第 $i$ 个苍蝇的坐标。

接下来一行有一个正整数 $K$ 表示多边形的点数。

以下 $K$ 行，每行两个正整数 $(X_i,Y_i)$，表示当苍蝇拍的第一个顶点的坐标为 $(X_1,Y_1)$ 的时候，其他顶点的坐标。各个顶点是顺次给出的。

输出格式

你需要输出有多少可行的放置苍蝇拍的方案。

输入输出样例 #1

输入 #1

4 5 2
1 3
3 4
4
0 0
2 0
2 2
0 2

输出 #1

4

输入输出样例 #2

输入 #2

5 5 3
1 4
1 3
2 2
3
4 7
6 3
7 6

输出 #2

3

输入输出样例 #3

输入 #3

6 7 2
2 5
4 5
8
1 4
3 3
4 1
5 3
7 4
5 5
4 7
3 5

输出 #3

1

说明/提示

样例解释

样例 1 解释

可以放置的苍蝇拍的位置如下：

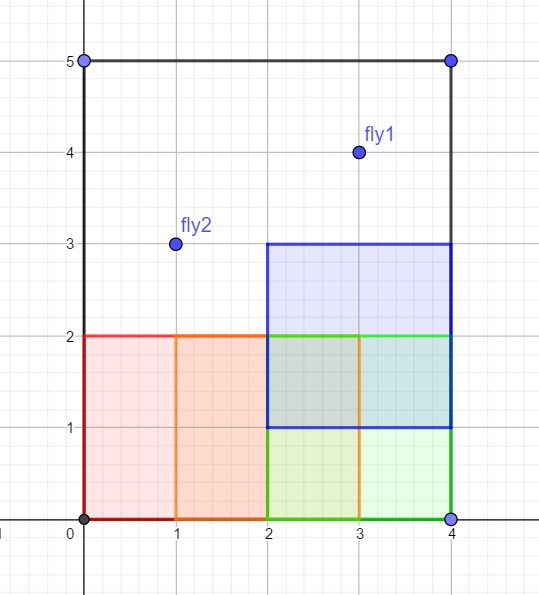
共 $4$ 种。

样例 2 解释

可以放置的苍蝇拍的位置如下：

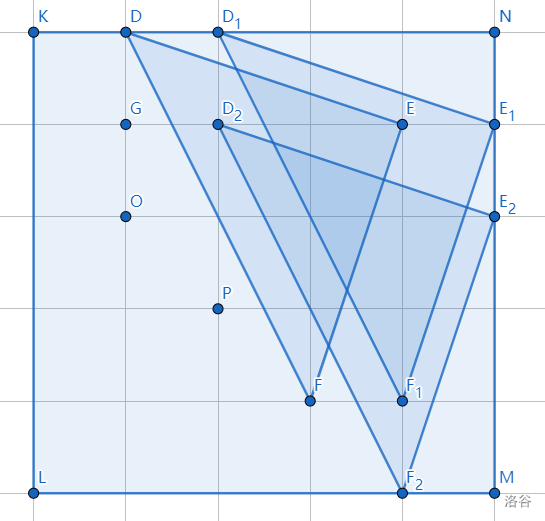
共 $3$ 种。

样例 3 解释

可以放置的苍蝇拍的位置如下：

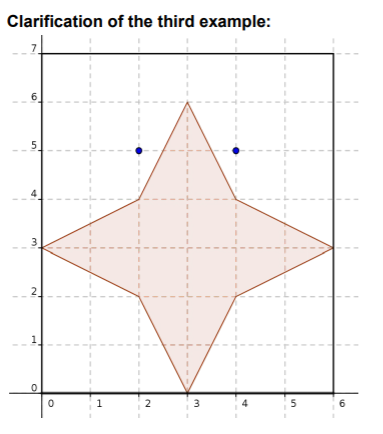
共 $1$ 种。

数据规模与约定

对于 $63\%$ 的数据，满足 $1\le X_p,Y_p\le 100$。

对于 $100\%$ 的数据，满足 $1\le X_p,Y_p\le 500,1\le N\le X_p\times Y_p,3\le K\le 10^4,0<X<X_p,0<Y<Y_p,-10^9\le X_i,Y_i\le 10^9$。

说明

题目译自 COCI2016-2017 CONTEST #3 T6 Meksikanac。

样例 1,2 的解释非官方

def is_on_segment(x, y, x1, y1, x2, y2):
    if x < min(x1, x2) or x > max(x1, x2):
        return False
    if y < min(y1, y2) or y > max(y1, y2):
        return False
    cross = (x2 - x1) * (y - y1) - (y2 - y1) * (x - x1)
    return cross == 0

def point_in_polygon(x, y, polygon):
    n = len(polygon)
    inside = False
    for i in range(n):
        p1 = polygon[i]
        p2 = polygon[(i + 1) % n]
        p1x, p1y = p1
        p2x, p2y = p2
        if (p1y > y) != (p2y > y):
            if p2y == p1y:
                continue
            t = (y - p1y) / (p2y - p1y)
            x_intersect = p1x + t * (p2x - p1x)
            if x < x_intersect:
                inside = not inside
    return inside

def is_point_in_or_on(x, y, polygon):
    for i in range(len(polygon)):
        p1 = polygon[i]
        p2 = polygon[(i + 1) % len(polygon)]
        if is_on_segment(x, y, p1[0], p1[1], p2[0], p2[1]):
            return True
    return point_in_polygon(x, y, polygon)

def main():
    import sys
    input = sys.stdin.read().split()
    idx = 0
    Xp = int(input[idx]); idx +=1
    Yp = int(input[idx]); idx +=1
    N = int(input[idx]); idx +=1
    flies = []
    for _ in range(N):
        x = int(input[idx]); idx +=1
        y = int(input[idx]); idx +=1
        flies.append((x, y))
    K = int(input[idx]); idx +=1
    polygon_original = []
    for _ in range(K):
        x = int(input[idx]); idx +=1
        y = int(input[idx]); idx +=1
        polygon_original.append((x, y))
    
    x0, y0 = polygon_original[0]
    dx = [x - x0 for x, _ in polygon_original]
    dy = [y - y0 for _, y in polygon_original]
    
    a_min_candidates = [-dxi for dxi in dx]
    a_min = max(a_min_candidates + [0])
    a_max_candidates = [Xp - dxi for dxi in dx]
    a_max = min(a_max_candidates + [Xp])
    
    b_min_candidates = [-dyi for dyi in dy]
    b_min = max(b_min_candidates + [0])
    b_max_candidates = [Yp - dyi for dyi in dy]
    b_max = min(b_max_candidates + [Yp])
    
    if a_min > a_max or b_min > b_max:
        print(0)
        return
    
    count = 0
    for a in range(a_min, a_max + 1):
        for b in range(b_min, b_max + 1):
            current_polygon = [(a + dx[i], b + dy[i]) for i in range(K)]
            valid = True
            for (x, y) in flies:
                if is_point_in_or_on(x, y, current_polygon):
                    valid = False
                    break
            if valid:
                count +=1
    print(count)

if __name__ == '__main__':
    main()