【动态规划】详解分组背包问题

JWASX

948人浏览 · 2025-03-16 13:57:17

JWASX · 2025-03-16 13:57:17 发布

1. 问题引入

本文前置文章：

下面是两种背包模式的区别：

0 - 1 背包 是说：有 n 个物品和一个重量为 t 的背包，这 n 个物品中第 i 个物品的重量为 w[i]，价值为 v[i]，那么这个背包能装下的物品最大价值是多少，注意一个物品只能选一次。
完全背包 是说：有 n 个物品和一个重量为 t 的背包，这 n 个物品中第 i 个物品的重量为 w[i]，价值为 v[i]，那么这个背包能装下的物品最大价值是多少，注意一个物品可以选无数次。

而分组背包跟前面两种也差不多，就是多了一个组的概念，问题描述起来就是：有 n 组物品和一个重量为 t 的背包，每个物品都有自己的体积，价值和组号，代表这个物品属于哪一组，要求在不超过背包容量的前提下，从每组物品中最多选择一个物品，使得背包中物品的总价值最大。

2. dp 公式

分组背包和 0-1 背包的遍历顺序没什么区别，只是 dp 公式有点不同，我们定义 dp[i][j] 为在前 i 组内每组只能选择一件商品且重量不超过 j 的前提下能获取的最大价值：
$dp[i][j]=\left\{ \begin{aligned} dp[i - 1][j]，不选择第 i 组的物品\\ dp[i-1][j - w[k]] + v[k]，选择第 i 组物品 \end{aligned} \right.$

如果不选择第 i 组物品，那么 $d p [i] [j] = d p [i - 1] [j]$ ，如果选择第 i 组物品，那么就是 $d p [i] [j] = d p [i - 1] [j - w [k]] + v [k]$ ，其中 k 是第 i 组里面的商品的下标，下面就以一道题目来讲述分组背包的代码。

3. 题目

来看一道洛谷的题目：P1757 通天之分组背包

3.1 二维数组解法

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int m = 0, n = 0;
        // arr[i][0]: i 物品的重量
        // arr[i][1]: i 物品的价值
        // arr[i][2]: i 物品的组数
        m = scanner.nextInt();
        n = scanner.nextInt();
        int[][] arr = new int[n + 1][3];
        for (int i = 1; i <= n; i++) {
            arr[i][0] = scanner.nextInt();
            arr[i][1] = scanner.nextInt();
            arr[i][2] = scanner.nextInt();
        }
        System.out.println(findMax(n, m, arr));
    }

    /**
     * @param n   n 件物品
     * @param m   背包重量为 m
     * @param arr 物品数组
     * @return
     */
    public static int findMax(int n, int m, int[][] arr) {
        // 首先将物品按照组号进行排序
        Arrays.sort(arr, 1, arr.length, (o1, o2) -> o1[2] - o2[2]);
        // 找出一共有多少组
        int count = 1;
        for (int i = 2; i <= n; i++) {
            if (arr[i][2] != arr[i - 1][2]) {
                count++;
            }
        }
        // dp[i][j]: 从下标 0-i 个组内各挑一件物品，在重量不超过 j 的前提下能够获取的最大收益
        int[][] dp = new int[count + 1][m + 1];
        // 遍历组
        int start = 1, end = 2;
        for (int i = 1; i <= count; i++) {
            // 从 [start, end - 1] 就是第 i 组的物品的范围
            while (end <= n && arr[end][2] == arr[end - 1][2]) {
                end++;
            }
            // dp[i][j]
            // 1.如果不选当前 i 组的物品，那么就是 dp[i-1][j]
            // 2.如果选当前 i 组的物品，那么就是 dp[i-1][j - arr[k][0]] + arr[k][1]
            // 对于二维数组遍历背包和遍历物品顺序没有区别
            // 先遍历背包
            for (int j = 0; j <= m; j++) {
                // 不选第 i 组的物品
                dp[i][j] = dp[i - 1][j];
                // 挨个遍历这个组内所有物品
                for (int k = start; k < end; k++) {
                    if (j >= arr[k][0]) {
                        dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - arr[k][0]] + arr[k][1]);
                    }
                }
            }
            start = end;
            end++;
        }
        return dp[count][m];
    }
}

上面是这道题目的二维数组解法，由于 dp 的定义，我们就必须提前求出来一共有多少组。

0-1 背包可以看作是特殊的分组背包，遍历顺序没什么区别，对于分组背包，物品就是分组，背包就是重量。这道题就是先遍历分组，然后找出这个组的所有下标范围，接着按照遍历背包，遍历物品的顺序来求出最大值。

for (int i = 1; i <= count; i++) 遍历分组
for (int j = 0; j <= m; j++) 遍历背包
for (int k = start; k < end; k++) 遍历物品

3.2 一维数组解法

一维数组写法就是空间压缩，为了方便看依赖，下面把 dp 的公式也粘贴下来：
$dp[i][j]=\left\{ \begin{aligned} dp[i - 1][j]，不选择第 i 组的物品\\ dp[i-1][j - w[k]] + v[k]，选择第 i 组物品 \end{aligned} \right.$
从上面的公式可以看出，dp[i][j] 是依赖正上方的格子和左上方的格子，比如下面图示。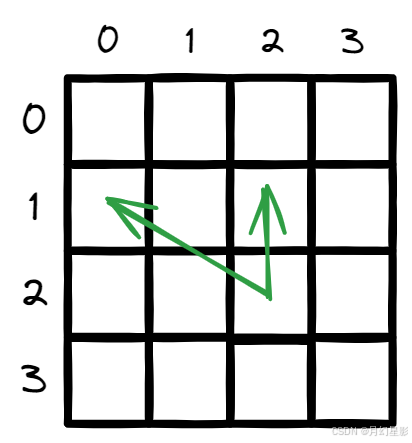
在这里插入图片描述
有了这个依赖关系，我们就可以给出一维数组的 dp 定义：

$d p [j] 表示重量不超过 j 的前提下能获取到的最大价值$

那么 dp 数组如何初始化呢？在二维数组遍历的时候就是全部初始化为 0，所以一维数组第一行也初始化为 0，如果按照二维数组的定义，那么一维数组初始化 dp[j] 的定义就是：第 0 组在容量不超过 j 的前提下能获取到的最大价值，当然了上面代码组是从 1 开始计算的，所以这里什么也不用做，直接初始化为 0 就行了。

如果说组号是从 0 开始，那么初始化也什么都不用做，直接也按 0-1 背包那样初始化为 0，因为我们计算肯定是从第一个组开始计算的。

/**
 * 空间压缩
 *
 * @param n   n 件物品
 * @param m   背包重量为 m
 * @param arr 物品数组
 * @return
 */
public static int findMax1(int n, int m, int[][] arr) {
    int[] dp = new int[m + 1];
    // 初始化为 0
    int start = 1, end = 2;
    // 找出一共有多少组
    int count = 1;
    for (int i = 2; i <= n; i++) {
        if (arr[i][2] != arr[i - 1][2]) {
            count++;
        }
    }
    for (int i = 1; i <= count; i++) {
        while (end <= n && arr[end][2] == arr[start][2]) {
            end++;
        }
        for (int j = m; j >= 0; j--) {
            for(int k = start; k < end; k++){
                if(j >= arr[k][0]){
                    dp[j] = Math.max(dp[j], dp[j - arr[k][0]] + arr[k][1]);
                }
            }
        }
        start = end;
        end++;
    }
    return dp[m];
}

4. 相关题目

2218. 从栈中取出 K 个硬币的最大面值和

一张桌子上总共有 n 个硬币栈。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的 顶部 取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在 恰好 进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少。

示例 1：

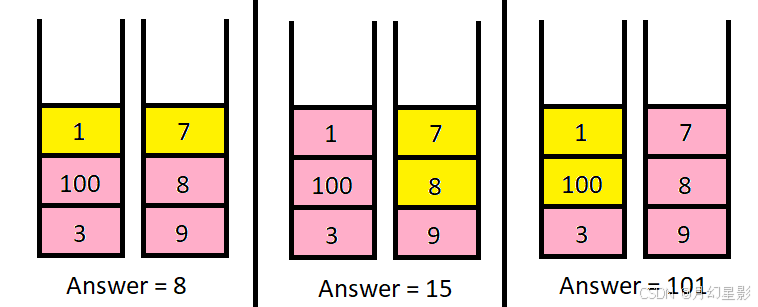
在这里插入图片描述

输入： piles = [[1,100,3],[7,8,9]], k = 2
输出： 101
解释：
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。

示例 2：

输入： piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
输出： 706
解释：
如果我们所有硬币都从最后一个栈中取，可以得到最大面值和。

提示：

$\mathrm n == \mathrm{piles.length}$
$1 <= n <= 1000$
$\mathrm{piles[i][j]} <= 10^5$
$\mathrm{1 <= k <= sum(piles[i].length) <= 2000}$

思路：

这道题关键是找出分组，什么才是一个分组，首先肯定不是硬币数，因为我可以每个栈都在顶部取一个硬币。

假设一个栈作为一个分组，那么在这个栈中的物品可以用银币数代替，比如上面图中第一个方案就是栈 1[1, 100, 3]，里面的物品就是（1，1），（2，101），（3，104），意思就是在这个栈中：

取 1 个硬币能收获 1 面值
取 2 个硬币能收获 101 面值
取 3 个硬币能收获 104 面值

所以按照这样的思路来看一个分组里面是不是只能取到一个方案，而刚好这个方案的硬币数就是重量，所以就能以这个思路来解题，由于题目连组数都给出来了，所以代码量比上面洛谷的题目还要少，分组还是以 1 开始，虽然上面题目是下标 0 开始，但是为了设置不取当前组方案的时候 dp[i][j] = dp[i-1][j]，以 i = 1 开始遍历能够避免边界判断。

class Solution {
    public int maxValueOfCoins(List<List<Integer>> piles, int m) {
        // 分组背包，每个背包的方案是一个分组，容量是 k，分组数就是栈的个数
        int n = piles.size();
        int[][] dp = new int[n + 1][m + 1];
        // 遍历分组
        for (int i = 1; i <= n; i++) {
            List<Integer> arr = piles.get(i - 1);
            // 求前缀和，也就是分组里面的物品
            int len = Math.min(m, arr.size());
            int[] preSum = new int[len + 1];
            for (int j = 1; j <= len; j++) {
                preSum[j] = preSum[j - 1] + arr.get(j - 1);
            }
            // 遍历背包
            for (int j = 0; j <= m; j++) {
                // 不获取当前组的方案
                dp[i][j] = dp[i-1][j];
                // 获取当前组的方案
                for (int k = 1; k <= Math.min(j, arr.size()); k++) {
                    dp[i][j] = Math.max(dp[i][j], dp[i-1][j - k] + preSum[k]);
                }
            }
        }
        return dp[n][m];
    }
}

顺便注意下里面判断的时候求前缀和和最后遍历方案都用了 Math.min(m, arr.size())，这个是因为如果 m 太小，但是一个栈里面有假设 1000 种方案，那么超过 m 的这部分根本就没必要计算。

上面是二维的版本，换成一维的如下。

class Solution {
    public int maxValueOfCoins(List<List<Integer>> piles, int m) {
        // 分组背包，每个背包的方案是一个分组，容量是 k，分组数就是栈的个数
        int n = piles.size();
        int[] dp = new int[m + 1];
        // 遍历分组
        for (int i = 1; i <= n; i++) {
            List<Integer> arr = piles.get(i - 1);
            // 求前缀和，也就是分组里面的物品
            int len = Math.min(m, arr.size());
            int[] preSum = new int[len + 1];
            for (int j = 1; j <= len; j++) {
                preSum[j] = preSum[j - 1] + arr.get(j - 1);
            }
            // 遍历背包
            for (int j = m; j >= 0; j--) {
                // 遍历方案
                for (int k = 1; k <= Math.min(j, arr.size()); k++) {
                    if(j >= k){
                        dp[j] = Math.max(dp[j], dp[j - k] + preSum[k]);
                    }
                }
            }
        }
        return dp[m];
    }
}