B2. Bouquet (Hard Version)

题目：

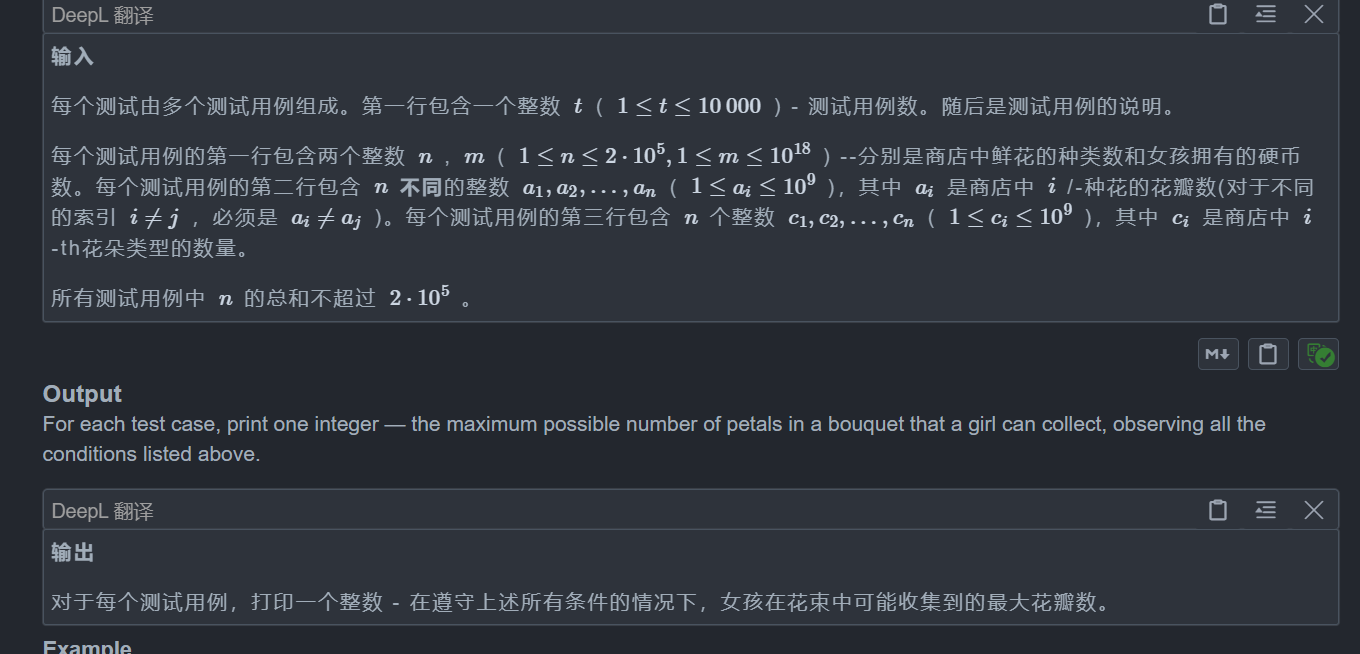
思路：

有点思维的模拟题

由于题目告诉我们每次选的花要确保任意两种之差都要小于等于 1（开始看错了）

也就是说我们只有 只选 x 或 选x和 x+1 这两种选法

我们如何选呢？

我们可以先只考虑选 x 的花，这样就有两种情况了

①.可以全选，即能够只选 x 花用完所有的钱 或 只选 x 花剩下的钱不能再买花了

②.不能全选，即选完 x 花后还剩下了很多钱可以用来买 x+1 花

这两种情况我们可以合并起来，一个显然的想法，如果我们要增加总价值，那么我们就要买 x+1 花，那买 x+1 花也有两种情况

①.如果能直接买，那就直接买

②.如果不能直接买，那就删一朵 x，再买一朵 x + 1

而这两种情况刚好与上面的两种情况相对应

也就是说我们现在的操作就是：先尽量买 x 花，如果有剩，看看能不能买 x+1 花，这样就达到了第一阶段的答案，随后我们再尝试将 x 花换成 x+1 花，最后将能换的都换完后就是第二阶段的答案了，显然第二次的答案一定大于第一次的答案，所以我们直接改变即可

具体实现看代码，有点小细节

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

void solve()
{
    int n, m;
    cin >> n >> m;
    vector<pair<int, int>> a(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i].first;
    }
    for (int i = 0; i < n; i++)
    {
        cin >> a[i].second;
    }
    sort(a.begin(), a.end());
    int res = 0;
    for (int i = 0; i < n; i++)
    {
        //只选一种
        int temp = min(m / a[i].first,a[i].second) * a[i].first;
        if (i + 1 < n && a[i + 1].first - 1 == a[i].first)
        {
            //选第一种的个数
            int getanum = min(m / a[i].first, a[i].second);
            //第二种能选的个数
            int getbnum = min((m - getanum * a[i].first) / a[i + 1].first, a[i + 1].second);
            temp += getbnum * a[i + 1].first;
            //剩下了多少钱
            int lastmoney = m - temp;
            temp += min(min(getanum, a[i + 1].second - getbnum),lastmoney);
        }
        res = max(temp, res);
    }
    cout << res << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

---

C. Squaring

题目：

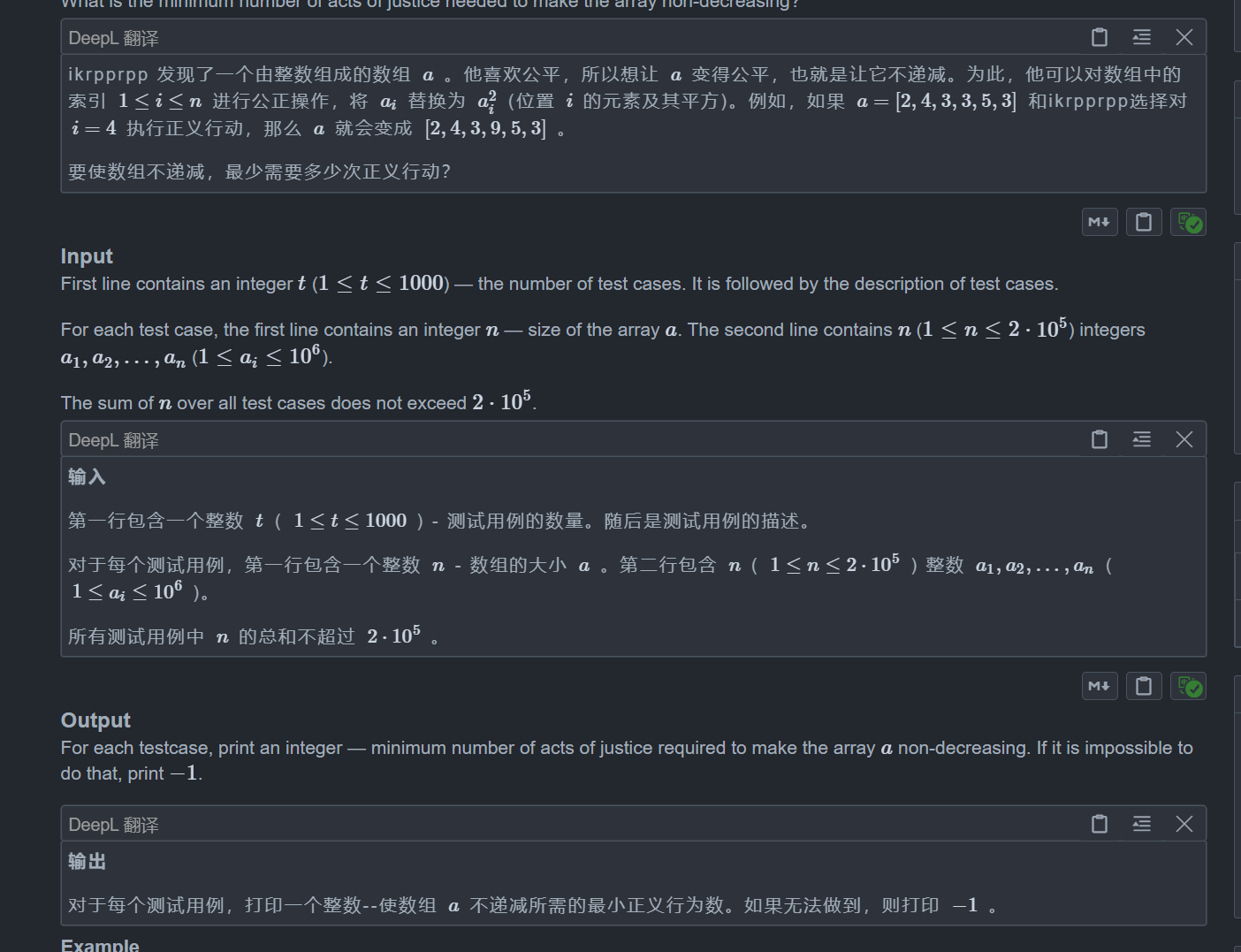
思路：

数学题

首先我们看无解的情况，显然就是当 1 前有个数比 1 大时，因为 1 的平方还是 1 ，所以无论操作多少次，我们都无法改变大小关系

其余情况显然有解，那么我们就来看如何计算

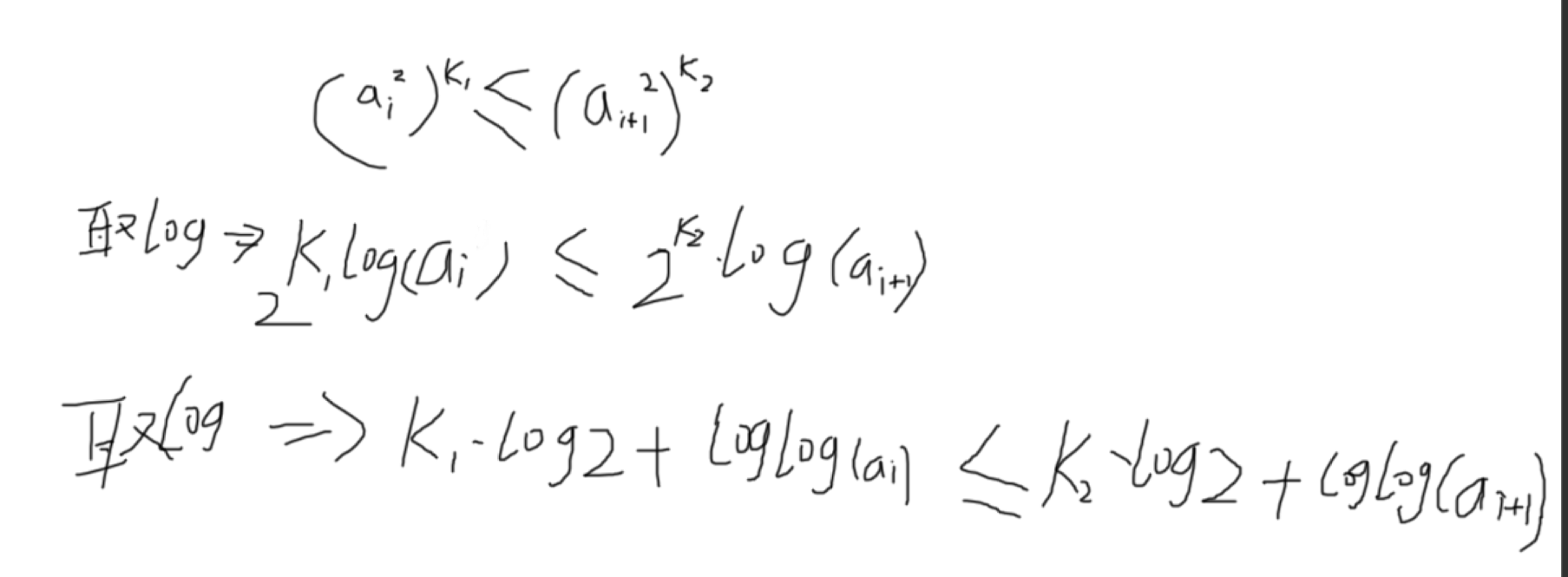
对于前后两个数，我们可以假设前面的数已经平方过 k1 次，我们当前数要平方 k2 次，那么就存在如上图所示的关系，由于我们如果用幂次的话绝对会爆数据，而我们并不需要知道具体的值，我们只需要知道大小关系，所以我们可以通过不断地取 log 来缩短数据大小，最后就是上图所示的关系

因此我们可以通过递推的方式通过上一个 k，来计算当前 k

如何计算呢？如果暴力枚举每次+1的话会超时（试过了）

因此我们考虑二分答案，特别的，在使用log时要记得减去 eps，不然精度会有问题

具体细节看代码 

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
const double eps = 1e-9;
const double lg2 = log(2);

void solve()
{
    int n, flag = 0;
    cin >> n;
    vector<int> a(n);
    vector<double> b(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
        if (i && a[i] == 1 && a[i] < a[i - 1])
            flag = 1;
        b[i] = log(log(a[i]*1.0));
    }
    if (flag)
    {
        cout << -1 << endl;
        return;
    }
    vector<int> f(n, 0);
    int res = 0;
    for (int i = 1; i < n; i++)
    {
        if (f[i - 1] * lg2 + b[i - 1] - eps > f[i] * lg2 + b[i])
        {
            int l = 0, r = 1e10;
            while (l + 1 < r)
            {
                int mid = l + r >> 1;;
                if (f[i - 1] * lg2 + b[i - 1] - eps > mid * lg2 + b[i])
                    l = mid;
                else
                    r = mid;
            }
            f[i] = r;
        }
        res += f[i];
    }
    cout << res << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}