2025第十六届蓝桥杯C++ B组题解
·
第十六届蓝桥杯C++ B组题解
洛谷评测链接:https://www.luogu.com.cn/problem/list?tag=363&page=4
A.移动距离
小明初始在二维平面的原点,他想前往坐标(233,666)。在移动过程中,他
只能采用以下两种移动方式,并且这两种移动方式可以交替、不限次数地使用:
- 水平向右移动,即沿着x轴正方向移动一定的距离。
- 沿着一个圆心在原点(0,0)、以他当前位置到原点的距离为半径的圆的圆
周移动,移动方向不限(即顺时针或逆时针移动不限)。
在这种条件下,他到达目的地最少移动多少单位距离?
你只需要输出答案四舍五入到整数的结果
思路
弧长+半径 弧度数 = 角度*半径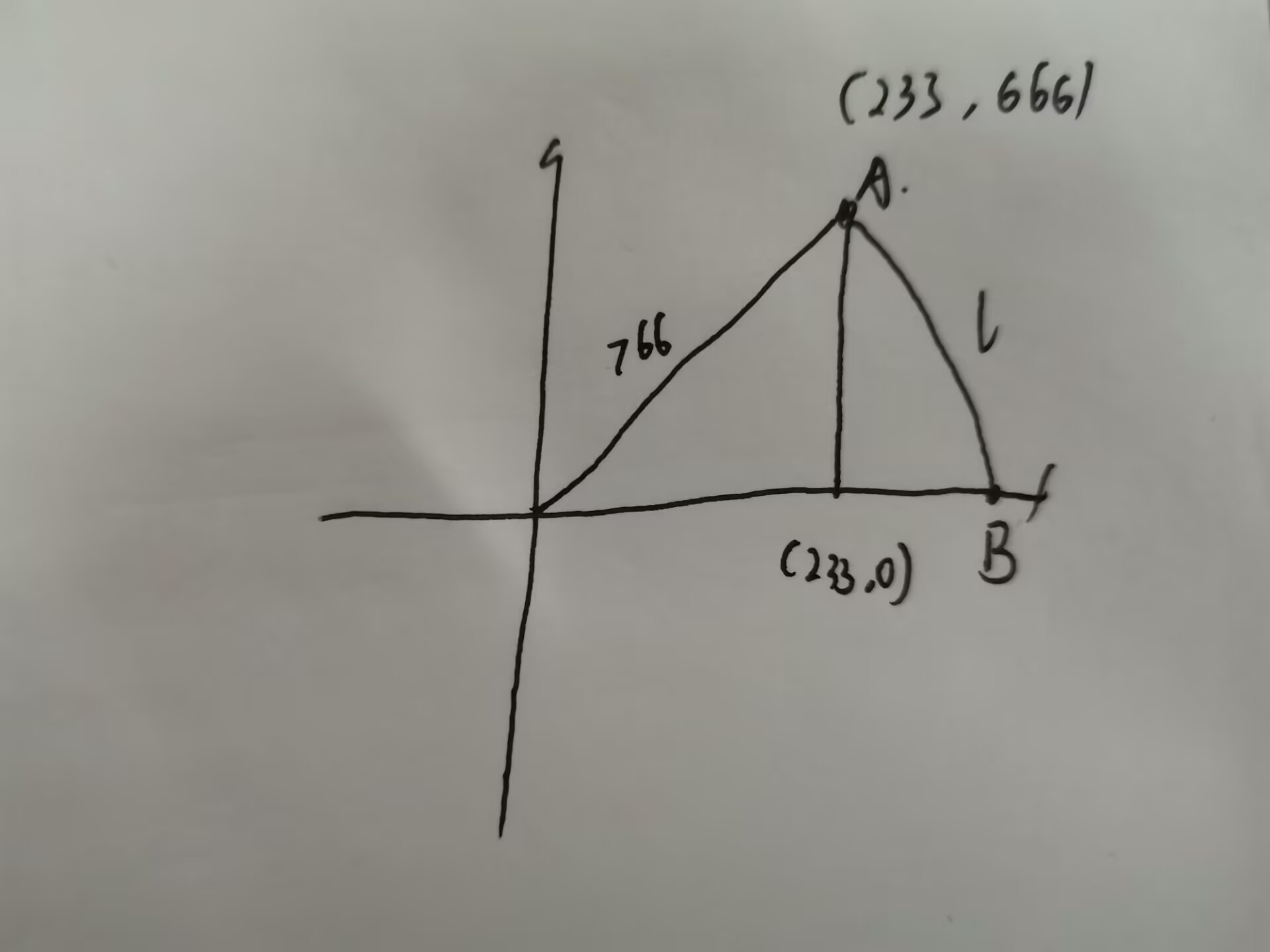

答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
int main(){
int x = 233;
int y = 666;
double res = atan(y*1.0/x);
cout<<(int)(res*sqrt(x*x+y*y)+sqrt(x*x+y*y))<<endl;
return 0;
}
B 客流量上限
一家连锁旅馆在全国拥有2025个分店,分别编号为1至2025。随着节日
临近,总部决定为每家分店设定每日客流量的上限,分别记作A1,A2,…,A2025。
这些上限并非随意分配,而是需要满足以下约束条件:
- A1,A2,…, A2025 必须是 1 至 2025 的一个排列,即每个 Ai 均是 1 至 2025
之间的整数,且所有Ai互不相同。 - 对于任意分店i和 j(1≤i, j≤2025,i 可等于 j),它们的客流量上限 Ai
和Aj 的乘积不得超过i× j+2025。
这些约束旨在平衡各分店客流压力,确保服务质量和运营稳定性。
现在,请你计算这样的分配方案究竟有多少种。由于答案可能很大,你只
需输出其对109+7取余后的结果即可
思路
全排列找规律 1 1 2 2 4 4 8 8 16 16
故答案为 2^(2025/2)
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
int a[15]={0,1,2,3,4,5,6,7,8,9,10,11,12,13};
int main(){
//枚举前11位
for(int z=1;z<=11;z++){
int res=0;
do{
int f = 0;
for(int i=1;i<=z;i++){
for(int j=1;j<=z;j++){
//判断是否合法
if(a[i]*a[j]>i*j+z) f=1;
}
}
if(!f) res++;
}while(next_permutation(a+1,a+z+1));
cout<<res<<" ";
}
return 0;
}
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
const int mod = 1e9+7;
int a[15]={0,1,2,3,4,5,6,7,8,9,10,11,12,13};
int main(){
ll n = 2025;
ll res=1;
ll k = n/2;
for(int i=1;i<=k;i++){
res=(res*2)%mod;
}
cout<<res%mod<<endl;
return 0;
}
C.可分解的正整数
【问题描述】
定义一种特殊的整数序列,这种序列由连续递增的整数组成,并满足以下
条件:
- 序列长度至少为3。
- 序列中的数字是连续递增的整数(即相邻元素之差为1),可以包括正整
数、负整数或0。
例如,[1,2,3]、[4,5,6,7] 和 [−1,0,1] 是符合条件的序列,而 [1,2](长度不
足)和[1,2,4](不连续)不符合要求。
现给定一组包含N 个正整数的数据A1,A2,…,AN。如果某个 Ai 能够表示
为符合上述条件的连续整数序列中所有元素的和,则称Ai是可分解的。
请你统计这组数据中可分解的正整数的数量
【输入格式】
输入的第一行包含一个正整数N,表示数据的个数。
第二行包含N个正整数A1,A2,…,AN,表示需要判断是否可分解的正整数
序列。
【输出格式】
输出一个整数,表示给定数据中可分解的正整数的数量。
【样例输入】
3
3 6 15
【样例输出】
3
思路
统计非1的数量
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
const int mod = 1e9+7;
int n;
int main(){
scanf("%d",&n);
int res=0;
for(int i=1;i<=n;i++){
int x;
cin>>x;
if(x!=1) res++;
}
cout<<res<<endl;
return 0;
}
D.产值调整


思路
找规律 经过几次变换后 A B C 会变为相同值
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
int pd(int a,int b){
double res = (a+b)/2;
res*=10;
return res/10;
}
void solve(){
int a,b,c,k;
cin>>a>>b>>c>>k;
int sa,sb,sc;
sa= a,sb=b,sc=c;
for(int i=0;i<k;i++){
if(sa==sb&&sb==sc){
break;
}
a = pd(sb,sc);
b = pd(sa,sc);
c = pd(sa,sb);
sa = a,sb = b,sc = c;
}
cout<<a<<" "<<b<<" "<<c<<endl;
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
E. 画展布置

思路
解法一 滑动窗口+差分+排序
解法二 前缀和 +排序
答案一
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
typedef long long ll;
ll a[N];
ll b[N];
int n,m;
int main(){
cin>>n>>m;
ll ans=0;
for(int i=1;i<=n;i++){
int x;
cin>>x;
a[i]=(ll)x*x;
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
b[i] = a[i]-a[i-1];
ans+=b[i];
}
ll sum = 0;
for(int i=1;i<=n;i++){
sum+=b[i];
if(i<m) continue;
ans = min(ans,sum-b[i-m+1]);
sum-=b[i-m+1];
}
cout<<ans<<endl;
return 0;
}
答案二
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
typedef long long ll;
ll a[N];
ll b[N];
int n,m;
int main(){
cin>>n>>m;
ll ans=1e18;
for(int i=1;i<=n;i++){
int x;
cin>>x;
a[i]=(ll)x*x;
}
sort(a+1,a+n+1);
ll sum = 0;
for(int i=m;i<=n;i++){
sum = a[i]-a[i-m+1];
ans = min(ans,sum);
}
cout<<ans<<endl;
return 0;
}
F. 水质检测

思路
贪心 + 动态规划
s1为第一行河床 s2 为第二行河床
d[0][i] 存储第一行到达i位置的最近检测器#的下表
d[1][i] 存储第二行到达i位置的最近检测器#的下表
故有4种情况
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
typedef long long ll;
string a,b;
int d[2][1000010];
int main(){
cin>>a>>b;
int res=0;
int t;
memset(d,-0x3f3f3f3f,sizeof(d));
for(int i=0;i<a.size();i++){
if(a[i]!='.'||b[i]!='.') {
if(a[i]!='.')
d[0][i] = i;
if(b[i]!='.')
d[1][i] = i;
t = i;
break;
}
}
for(int i=t+1;i<a.size();i++){
if(a[i]=='#'&&b[i]=='#'){
d[0][i] = i;
d[1][i] = i;
res+=min(i-d[0][i-1]-1,i-d[1][i-1]-1);
continue;
}
if(a[i]=='#'&&b[i]=='.'){
if(i-d[0][i-1]-1<i-d[1][i-1]) {
d[0][i] = i;
d[1][i] = d[1][i-1];
}
else {
d[0][i] = i;
d[1][i] = i;
}
res+=min(i-d[0][i-1]-1,i-d[1][i-1]);
continue;
}
if(a[i]=='.'&&b[i]=='#'){
if(i-d[1][i-1]-1<i-d[0][i-1]){
d[0][i] = d[0][i-1];
d[1][i] = i;
}
else{
d[0][i] = i;
d[1][i] = i;
}
res+=min(i-d[0][i-1],i-d[1][i-1]-1);
continue;
}
d[0][i] = d[0][i-1];
d[1][i] = d[1][i-1];
}
cout<<res<<endl;
return 0;
}
G. 生产车间

思路
树形dp
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+10;
typedef long long ll;
int n;
int a[N], dp[N][N];
vector<int> g[N];
int res;
void dfs(int x, int fa, int val){
if(g[x].size() == 1 && g[x][0] == fa){
dp[x][a[x]] = a[x];
return;
}
for(int i = 0;i<g[x].size();i++){
int j = g[x][i];
if(j == fa) continue;
dfs(j, x, min(val,a[j]));
for(int z = val;z >= 0; --z){
for(int k = 0;k <= min(a[j], z); ++k){
dp[x][z]= max(dp[x][z-k] + dp[j][k], dp[x][z]);
res = max(dp[x][z], res);
}
}
}
return;
}
int main(){
cin >> n;
for(int i = 1;i <= n; ++i) cin >> a[i];
int x, y;
for(int i = 1;i < n; ++i){
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs(1, 1, a[1]);
cout << res <<endl;
return 0;
}
H. 装修报价
未完待续…
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)