so，既然递推非常重要，那么递归肯定也同样重要；递推是从前往后推，那么递归就是从后往前推~~；递推难倒一大片，那么递归也会难倒一大片~~。既然递归是从后往前推，那么就要讲到递归最主要的特点了：函数自调用。其中呢，直接调用是指a调用a，也就是自己用自己用自己...；间接调用呢就是a调用b，b调用a，也就是我用你用我用你用我用你...

如果还有点不懂的话，那就看题吧（后面的dfs是递归函数，没有特殊意义，后面还有bfs广搜哈）

2.例题

1.给定一个整数n（n≥1），用递归求1+2+3+...+(n-1)+n

这道题呢，既然要用递归，我们要知道一个概念：递归有三个条件，分别是题目为累加问题、有递归条件且有限、有递归边界，可以发现，这道题刚好符合（累加，递归条件往下走且有限，有边界）

继续分析，我们发现递归条件就是这一层的数加上比这一层数少的所有数之和，也就是 $a_n = n+a_{n-1}$

而边界呢，自然也就是n=1时 $a_n$ =1啦

所以快速解决：

#include <bits/stdc++.h>
using namespace std;

int n;

int dfs(int n){          //函数看得懂吧
	if(n == 1) return 1; //边界
	return n+dfs(n-1);   //条件，也就是自调用
}

int main(){
	cin >> n;
	cout << dfs(n);     //int型函数直接输出即可
	return 0;           //好习惯是在实践中养成的（虽然我不喜欢写doge）
}

简单吧，事实上递归使用栈来存储的，至于栈么，欲知后事如何，且听n*下回分解哈~

好，进入第二题。

2.设有n个数(1 ≤ n ≤ 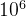$10^{6}$ )已经按照从大到小的顺序排列，现输入一个x，判断x是否在这n个数中，如在，则输出“YES”，否则输出“NO”。

第一行输入n,x，代表有多少数和待查找数。

第二行是n个整数，代表每个数的值。

输出“YES”或“NO”，代表x是否在这n个数内。

样例输入：

5 10

1 7 89 32 10

样例输出：

YES

好，看到这道题我们会发现是一道查找问题，当然，binary_search和upper/lower_bound这种二分的方法先不说哈，有点太没意思了。后面将会有拓展二分算法，有兴趣等吧o(*￣︶￣*)o。

我们数据查找无非就两种：顺序查找（也就是一个一个找，用循环可以，但不讲）和二分查找，因为二分是在排好序的情况下能用的，so我们题干中因为已给定从大到小，那么就可以用二分啦（sort+二分去一边吧）。

我们来构建一下二分的大模型：

我们用L来作为数组a最前端的界限，R来作为数组最尾端的界限，mid作为L~R的中间项，那么如果：

1.当待查找数x == a[mid]时，直接输出“YES”

2.当x < a[mid]时，就把L提到mid的位置，向后找，也就是R不变，L = mid+1，mid=新的L~R的中间项

3.当x > a[mid]时，就把R提到mid的位置，向前找，也就是L不变，R = mid-1，mid=新的L~R的中间项

4.最后当L ≥ R时还没有找到，也就是数组中没有x，输出“NO”

这样的话可以发现有循环的条件、边界以及类似累加的算法，递归起。

#include <bits/stdc++.h>
using namespace std;

int n,x,l,r,mid,a[1000005];  //a数组的大小为1000000，本人习惯从a[1]开始输入，所以开了+5保险，但至少需要+1

void dfs(int x,int l,int r){     //这里void类型不返回值，但正常情况要加return;/exit(0);
	//这里的x,l,r是局部变量，会覆盖全局变量x,l,r，但尽量还是不要像我这样写哈~
	if(l <= r){
		mid = (l+r)/2;
		if(a[mid]==x){
			cout << "YES";
			return;
		} 
		else if(a[mid] > x){
			dfs(x,mid+1,r);
		}
		else{
			dfs(x,l,mid-1);
		}
	}
	else cout << "NO";
}

int main(){
	cin >> n >> x;
	for(int i = 1;i <= n;i++){
		cin >> a[i];
	}
	l=1,r=n;
	dfs(x,l,r);
	return 0;
}

好，结束，接下来又是老朋友了。

3.汉诺塔问题

这题目可以说老的不能再老了，还有上章递推算法（基础算法）中也讲过了，去年CSP这递归5道错了俩，无缘复赛┭┮﹏┭┮

于是呢，我狂补几个月，so这汉诺塔问题吧，so ~~difficult~~ easy，轻松一学就~~还是没会~~拿下了。

好，看题：（这里不全抄了，反正都不知道讲过多少遍了，就讲些改动的~~说实话没改~~）

n个圆盘中以半径从大到小、从下往上套在a柱上，每次只允许移动每个柱子上最上面的圆盘到另外两个中的一个上（有a,b,c三个柱子），但不允许大盘子在小盘子之上，现要求求出有多少种方法将a柱的盘子全部移到c柱上。

咳咳，看见红色斜体字了叭。这明显是一道累加题，且条件是一个盘子从a到b/c，b到a/c，c到a/b，边界就是n个圆盘全部到c盘上。递归来吧~

我们先列举几个看看：

n=1 $a\rightarrow c$ 一次

n=2 $a\rightarrow 1\rightarrow b,a\rightarrow 2\rightarrow c,b\rightarrow 1\rightarrow c$ 三次

n=3时就是7步（不想列了，累，请不知如何推导的读者尝试写下来吧）

这里我们把第3、4、7步列出来，就会发现一个神奇的现象（自己列出来吧）：

n=2时的3步与拎出来的这3步是几乎一样的，只是盘1和盘2打包带走了。

由此，我们可得：（以优先级排序）

①当n=0时，结束程序，否则继续；

②用c柱作为过渡，将a柱的n-1片圆盘移到b柱上，用dfs(n-1,a,b,c)即可；

③将a柱剩下的最大的一片移到c柱上；

④用a柱作为过渡，将b柱上的n-1片圆盘移到c柱上，即dfs(n-1,b,c,a)。

0k，分析到这里，我们直接上代码：

#include <bits/stdc++.h>
using namespace std;

int n,step;

void dfs(int n,char a,char b,char c){
	if(n == 0) return;                  //第①步
	dfs(n-1,a,c,b);                     //第②步
	step++;                             //第③步移最大圆片时+1
	dfs(n-1,b,c,a);						//第④步
}

int main(){
	cin >> n;
	dfs(n,'a','b','c');                 //a,b,c仅作为塔名，方便处理
	cout << step;
	return 0;
}

我们这个代码中其实每一次调用圆片数量就少了一个，这样一直到n=0时便直接退出，也算轻松解决吧~

好，下一题又又又出现了，斐波那契，开！！（魔怔了）

4.又又又又又又出现的斐波那契

好，老生常谈，不讲题目了，直接讲思路。

这里斐波那契从我们第n项往前推就成了一个典型的递归（说实话本来想放在第一题讲的），递推公式就是 $f_n = f_{n-1} + f_{n-2}$ ,边界就是 $f(1) = 1,f(0) = 0$ （这里0主要用来特判）

好，那这样的话也是很简单了，带过：

#include <bits/stdc++.h>
using namespace std;

int n;

int dfs(int n){
	if(n == 0) return 0;
	if(n == 1) return 1;
	return dfs(n-1)+dfs(n-2);
}

int main(){
	cin >> n;
	cout << dfs(n);
	return 0;
}
//注意这里n值不能过大，不然会超时，若要让n值更大，就用原来讲过的记忆化搜索：
/*
#include <bits/stdc++.h>
using namespace std;

long long n,f[55];

long long dfs(long long n){
	if(f[n]) return f[n];
	if(n == 0) return 0;
	if(n == 1) return 1;
	return f[n] = dfs(n-1)+dfs(n-2);
}

int main(){
	cin >> n;
	cout << dfs(n);
	return 0;
}
*/

快速跳转至记忆化搜索

好的，这里根据书本内容涉及了集合的内容，由于实在看不懂，所以不好给大家讲，给大家看一下题目就过了叭(。・＿・。)ﾉI’m sorry~：

5.集合划分

已知S是一个具有n个元素的集合, $S = \left \{ a_1,a_2,a_3,...,a_n \right \}$ ,现将S划分成k个满足下列条件的子集和S1,S2,...,Sk，且满足：

$1.S_i \neq \varnothing$

$2.S_i \cap S_j = \varnothing$

$3.S1\cup S2\cup S3\cup ...\cup Sk = S$

则称S1,S2,S3,...,Sk是集合S的一个划分。它相当于把S集合中n个元素放入k个无标号的盒子中，使得没有一个盒子为空。请确定集合S的划分数S(n,k)。

输入样例：

10 6

输出样例：

22827

#include <bits/stdc++.h>
using namespace std;

int n,k;                            //当输入的比较大时，需用高精度计算

int dfs(int n,int k){
	if(n < k || k == 0) return 0;
	if(k == 1 || k == n) return 1;
	return dfs(n-1,k-1)+k*s(n-1,k);
}

int main(){
	cin >> n >> k;
	cout << dfs(n);
	return 0;
}

快速跳转至高精度算法

下一道题呢，比较简单。

6.数的计数（Noip2001）

这题要求我们找出1~n中具有以下性质数的个数（包括n）。输入一个自然数n（n ≤ 1000），然后对此自然数做如下处理：

不作任何处理；在它的左边加上一个自然数，但这个自然数要 ≤ ½n，加上此数后，继续以此类推，直至不能再加。

这题呢，我们可以用递归哈，公式不推了，直接写： $f(n) = f(1)+f(2)+...+f(n/2)$

（注：当n较大时会超时，时间呈指数级）

#include <bits/stdc++.h>
using namespace std;

int n,ans;                            

void dfs(int n){
	ans++;
	for(int i = 1;i <= n/2;i++){
		dfs(i);
	}
}

int main(){
	int n;
	cin >> n;
	dfs(n);
	cout << ans;
	return 0;
}

当然，我们在数据较大时肯定不能这么做，所以用记忆化增加减少时间，来吧：

#include <bits/stdc++.h>
using namespace std;

int n,h[1005];                            

void dfs(int n){
	if(h[n] != -1) return;
	h[n] = 1;
	for(int i = 1;i <= n/2;i++){
		dfs(i);
		h[n] += h[i];
	}
}

int main(){
	int n;
	cin >> n;
	memset(h,-1,sizeof(h));       //注意初始化
	dfs(n);
	cout << h[n];
	return 0;
}

拿下，当然，还有三种算法，这里不展开讨论，大家有兴趣可以试一试哈~

好了，最后给大家布置三道习题：

3.习题

1.爬楼梯

小明爬一个有n（1 ≤ n ≤ 30）级的楼梯，每次可以越1级或2级，输入n，求有多少种方法走完楼梯。

输入样例：

输出样例：

2.[NOIP 1998 普及组] 幂次方

题目描述

任何一个正整数都可以用 2 的幂次方表示。例如 137=27+23+20。

同时约定次方用括号来表示，即 ab 可表示为 a(b)。

由此可知，137 可表示为 2(7)+2(3)+2(0)

进一步：

7=22+2+20 ( 21 用 2 表示)，并且 3=2+20。

所以最后 137 可表示为 2(2(2)+2+2(0))+2(2+2(0))+2(0)。

又如 1315=210+28+25+2+1

所以 1315 最后可表示为 2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)。

输入格式

一行一个正整数 n。

输出格式

符合约定的 n 的 0,2 表示（在表示中不能有空格）。

输入输出样例

输入 #1

输出 #1

2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)

说明/提示

【数据范围】

对于 100% 的数据，1≤n≤2×104。

NOIP1998 普及组第三题

3.因子分解

输入一个数，输出其分解质因数后的结果。

输入样例：

输出样例：

60 = 2^2*3*5

4.总结

递归也算是很重要的一部分了，这里本蒟蒻还没有展开讲step类型回归等算法，可以说是非常庞大的一个算法分支了，希望大家有空能多了解这种算法，扎实基础，加油！！

（做了4小时，累了，没那么展开讲，有错误的地方希望能及时提醒，谅解！）

信息学奥赛社区

集算法之大成！助力oier实现梦想！

更多推荐

【近一个月的学习记录】

信息学奥赛社区

导弹拦截（排序）

经过 11 年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为 0 时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷：每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导

信息学奥赛社区

luogu 题解：P1027 [NOIP 2001 提高组] Car 的旅行路线

剩下的很显然，计算同一个矩形中两点间的“高速公路”的边权并记录，计算不同矩形的两点间的“航线”的边权并记录，跑 floyd 即可，最后枚举起点与终点的状态。但是由于题目只给出了矩形的三个顶点的坐标，第四个顶点应该自己计算。声明：为了提高代码可读性，此代码采用了 AI 重构。个点，考虑用邻接表、floyd 算法解决此题。一种很显然的做法，注意到数据规模。种不同的状态（矩形的四个顶点）。考虑拆点，拆点