经过 11 年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为 0 时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷：每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。

某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹，请计算这一天的最小使用代价。

输入格式

第一行包含 4 个整数 x1​,y1​,x2​,y2​，每两个整数之间用一个空格隔开，表示这两套导弹拦截系统的坐标分别为 (x1​,y1​),(x2​,y2​)。第二行包含 1 个整数 N，表示有 N 颗导弹。接下来 N 行，每行两个整数 x,y，中间用一个空格隔开，表示一颗导弹的坐标 (x,y)。不同导弹的坐标可能相同。

输出格式

一个整数，即当天的最小使用代价。

输入输出样例

输入 #1复制

0 0 10 0
2
-3 3
10 0

输出 #1复制

18

输入 #2复制

0 0 6 0
5
-4 -2
-2 3
4 0
6 -2
9 1

输出 #2复制

30

说明/提示

两个点 (x1​,y1​),(x2​,y2​) 之间距离的平方是 (x1​−x2​)2+(y1​−y2​)2。

两套系统工作半径 r1​,r2​ 的平方和，是指 r1​,r2​ 分别取平方后再求和，即 r12​+r22​。

样例 1 说明

样例 1 中要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为 18 和 0。

样例 2 说明

样例 2 中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为 20 和 10。

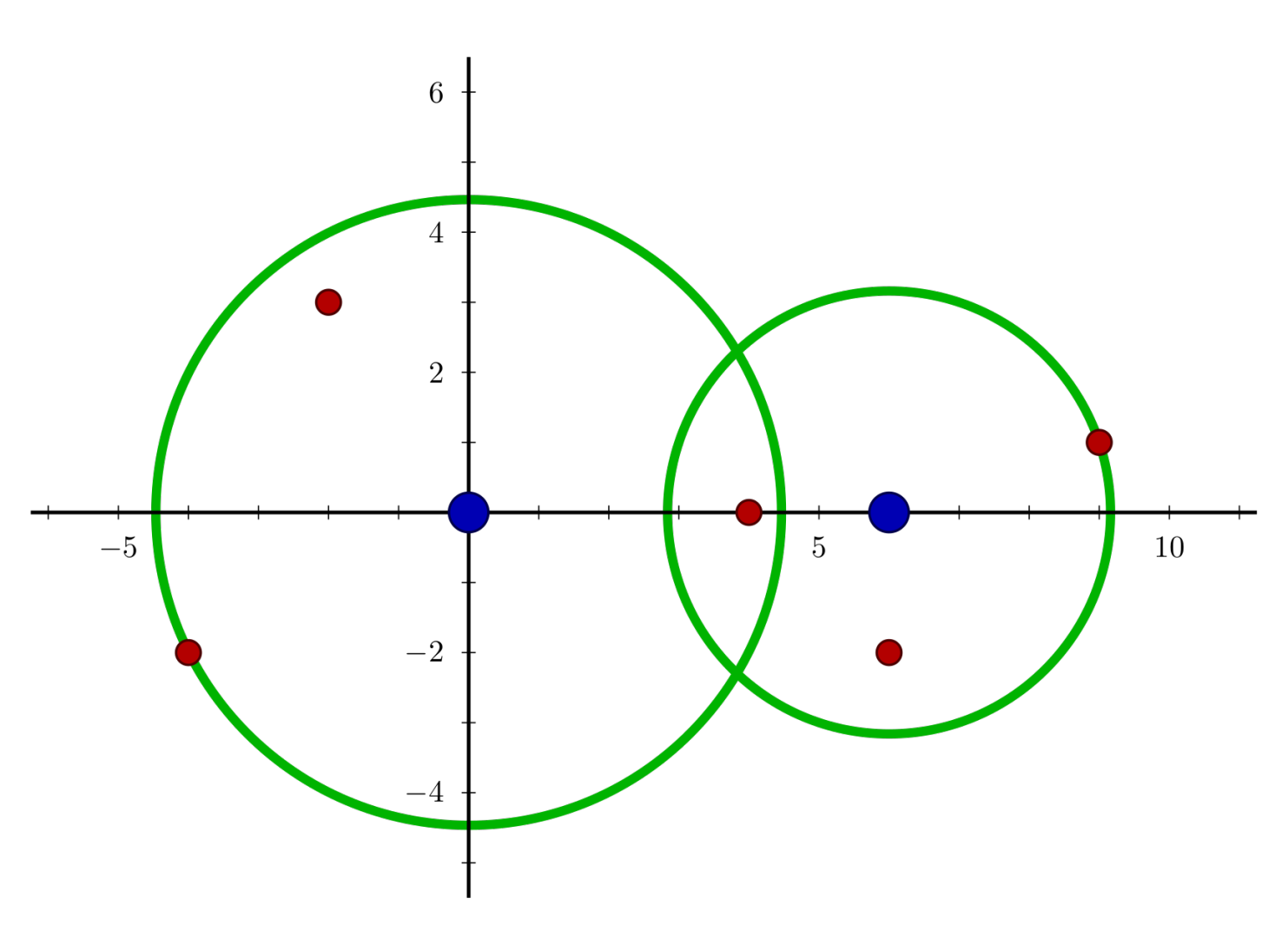
【数据范围】。

• 对于 10% 的数据，N=1。
• 对于 20% 的数据，1≤N≤2。
• 对于 40% 的数据，1≤N≤100。
• 对于 70% 的数据，1≤N≤1000。
• 对于 100% 的数据，1≤N≤105，且所有坐标分量的绝对值都不超过 1000。

NOIP2010 普及组 第三题

这道题整篇题目及附加图都看起来跟解析几何有关，不妨往这上面想一想。下文把一个设备的导弹拦截范围抽象成一个圆，把导弹抽象成一个点。

首先，有一个贪心的想法，就是让两个圆的半径尽量小（非常明显，过一下步骤，不过多赘述）。那么就只对于一个圆，是不是就只需要看离圆心距离最远的那个点，以那个点到圆心的距离为半径。可这道题有两个圆，我们的脑瓜只会处理一个圆。那我们就看看算法标签“排序”，是不是我们只需要对每个点到指定的一个圆（以下简称圆一）的圆心的距离从大到小排序，在循环遍历一下，处理另一个圆（以下简称圆二），当遍历到 i 时 ( 1<=i<=N ) ，让圆一处理第 i+1 个点到第 N 个点，让圆二处理前面的。因为我们按点到圆一的圆心距离排了序的，再结合上面对于一个圆的处理方法，它的半径就是排序后第 i+1 个点到它圆心的距离。而圆二就可以用一个变量去存储前 i 个点到圆二圆心的距离的最大值，它的半径就是这个变量。每次处理时，代价就是半径的平方和，用一个变量来存这些代价的最小值，这就是答案。

其次，计算过程中不是有个点到点的距离吗？公式中有根号，但结果要平方，那就可以在计算的时候就存距离的平方，答案也直接存变量的和不用平方了，就不会有根号带来的精度问题。

完整代码奉上。

#include<bits/stdc++.h>

#define int long long

using namespace std;

int num1_x,num2_x,num1_y,num2_y,r,ans=0x3f3f3f3f3f3f3f3f,n;

const int N=1e5+10;

struct Node{//结构体存到两圆心的距离的平方

    int num1,num2;

}a[N];

bool cmp(Node f,Node g){//排序按到圆一的距离的平方从大到小

    return f.num1>g.num1;

}

signed main(){

    ios::sync_with_stdio(false);

    cin.tie(0);

    cout.tie(0);

    cin>>num1_x>>num1_y>>num2_x>>num2_y>>n;

    for(int i=1;i<=n;i++){

        int num1,num2;

        cin>>num1>>num2;

        a[i].num1=(num1_x-num1)*(num1_x-num1)+(num1_y-num2)*(num1_y-num2);//两点之间的距离公式是sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))，用勾股定理推的，可以画个平面直角坐标系看。我这里直接平方了，去了根号。

        a[i].num2=(num2_x-num1)*(num2_x-num1)+(num2_y-num2)*(num2_y-num2);//同理

    }

    sort(a+1,a+n+1,cmp);//排序

    ans=a[1].num1;

    for(int i=1;i<=n;i++){

        r=max(r,a[i].num2);//圆二半径的平方

        ans=min(a[i+1].num1/*圆一半径的平方*/+r,ans);

    }

    cout<<ans;//半径平方和的最小值

    return 0;

}