一、排列和排列数

(1)排列：从 n 个不同元素中，任取 m(m≤n)个元素，按照一定的顺序排成一列，叫做从 n 个不同元素中取出 m 个元素的一个排列。

    如果两个排列相同，不仅这两个排列的元素必须完全相同，排列的顺序也必须完全相同。

 

(2)排列数：从 n 个不同元素中取出 m(m≤n)个元素的所有排列,

排列的记号和公式为：

 

 

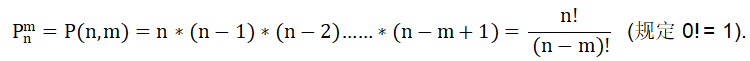
当 m＝n 时，为全排列

 

问题：

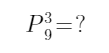
10个同学，选4个人，按选出的顺序排成一列，有多少种选法？

 

 

二、组合和组合数

(1)组合：从 n 个不同元素中，任取 m(m≤n)个元素并成一组，叫做从 n 个不同元素中取出 m 个元素的一个组合。

如果两个组合中的元素完全相同，不管元素的顺序如何，都是相同的组合；只有当两个组合中的元素不完全相同时，才是不同的组合。

 

(2) 组合数：从 n 个不同元素中取出 m(m≤n)个元素的所有组合的个数，

排列的记号和公式为：

 

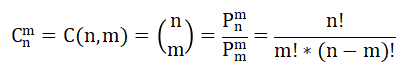
组合数的性质1: 

组合数的性质２:

 

 

问题：

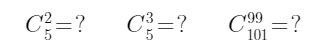
10个同学，选4个人去值日，有多少种选法？

---

捆绑

例题：4人排成一队，甲和乙必须相邻，有多少种排队方法？

【答案与分析】把甲乙捆绑，和另外两人排列。P(3,3)*2=12。

 

插空

例题：某人射击8枪，命中4枪，恰好有3枪连续命中，有多少种不同的情况？

【答案与分析】20。

分析：因为连续命中的三枪与单独命中的一枪不能相邻，因而这是一个插空问题。另外没有命中的之间没有区别，不必计数。

即在四发空枪之间形成的5个空中选出2个的排列，即 P(5,2)。